Microwave-to-Optical Transduction
•
Microwave-through-Optical Entanglement
•
Optical-to-Microwave Control
•

Stefan Krastanov | MIT ⟶ UMass Amherst

Entanglement

Alice has a qubit
Alice has a qubit
Bob too
They can be entangled! \[\begin{aligned} A=|\phi_{+}\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ B=|\psi_{-}\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}}\\ C=|\psi_{+}\rangle=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ D=|\phi_{-}\rangle=\frac{|00\rangle-|11\rangle}{\sqrt{2}} \end{aligned}\]
They can be entangled! \[\begin{aligned} A=|\phi_{+}\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ B=|\psi_{-}\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}}\\ C=|\psi_{+}\rangle=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ D=|\phi_{-}\rangle=\frac{|00\rangle-|11\rangle}{\sqrt{2}} \end{aligned}\]
Hidden Variable theories¹
  1. Krastanov et al.
    Art installation on Non-contextual Hidden Variable theories

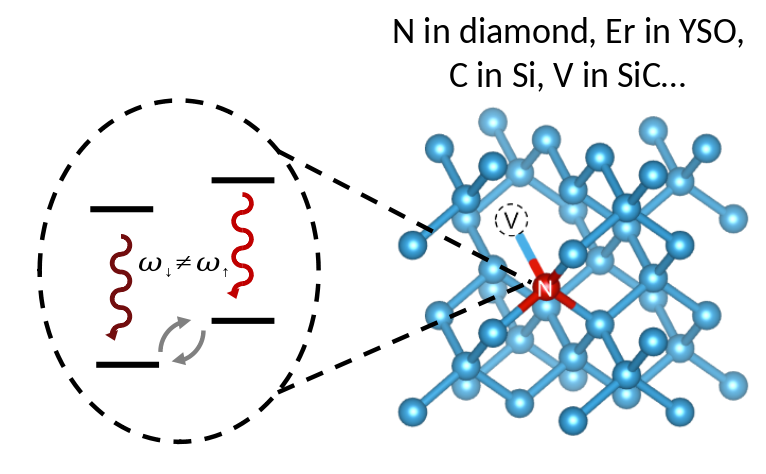
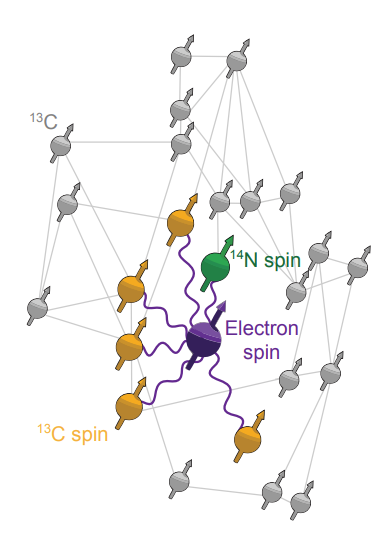
Entanglement with Color Centers

The Color Center

(Optical) Electronic Spin for Networking
(Microwave) Nuclear Spin for Memory

Entanglement Protocols

Inherently low probability of success (DLCZ-like)

Full excitation and path erasure (Barret-Kok)

Single-photon reflection

Atom-photon gates (Duan-Kimble)

Low-probability of success (DLCZ-like)

Full excitation and path erasure (Barret-Kok)

Single-photon reflection

Atom-photon gates (Duan-Kimble)

Rate only classical light no optical excitation
DLCZ \( \eta (1-F) \) ✅ ❌
BK \( \eta^2 \) ✅ ❌
reflection \( \eta^2 \) ❌ ✅

You also need a color center that does not suffer from spectral diffusion or charge state instabilities.

If you end up with significant optical excitation, you also need a way to turn off the hyperfine coupling to the (nuclear) memory.

Entangling Transmons or other MW qubits

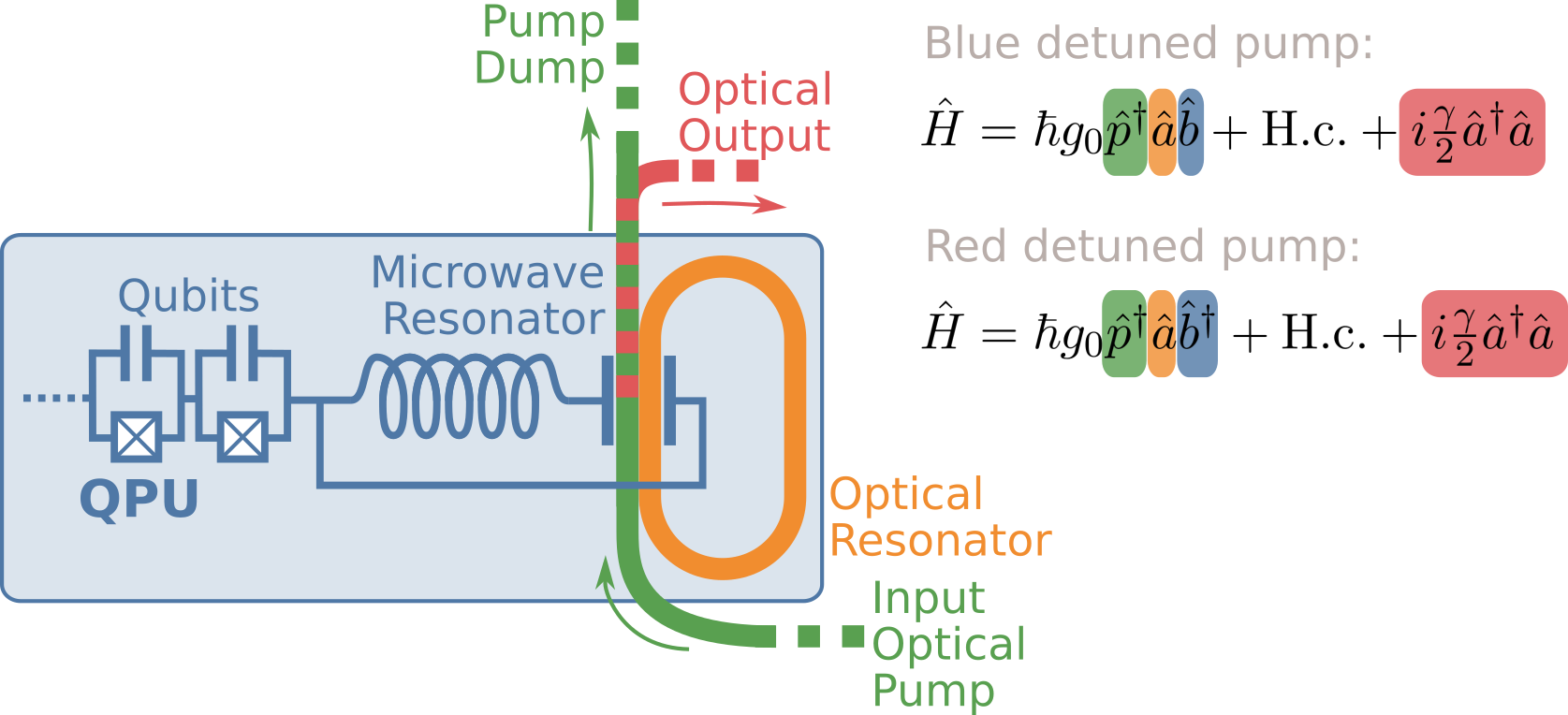
Deterministic Transduction

Transduction Hardware
Transduction Protocol

Probabilistic Heralding

Why are color-center folks never talking about transduction...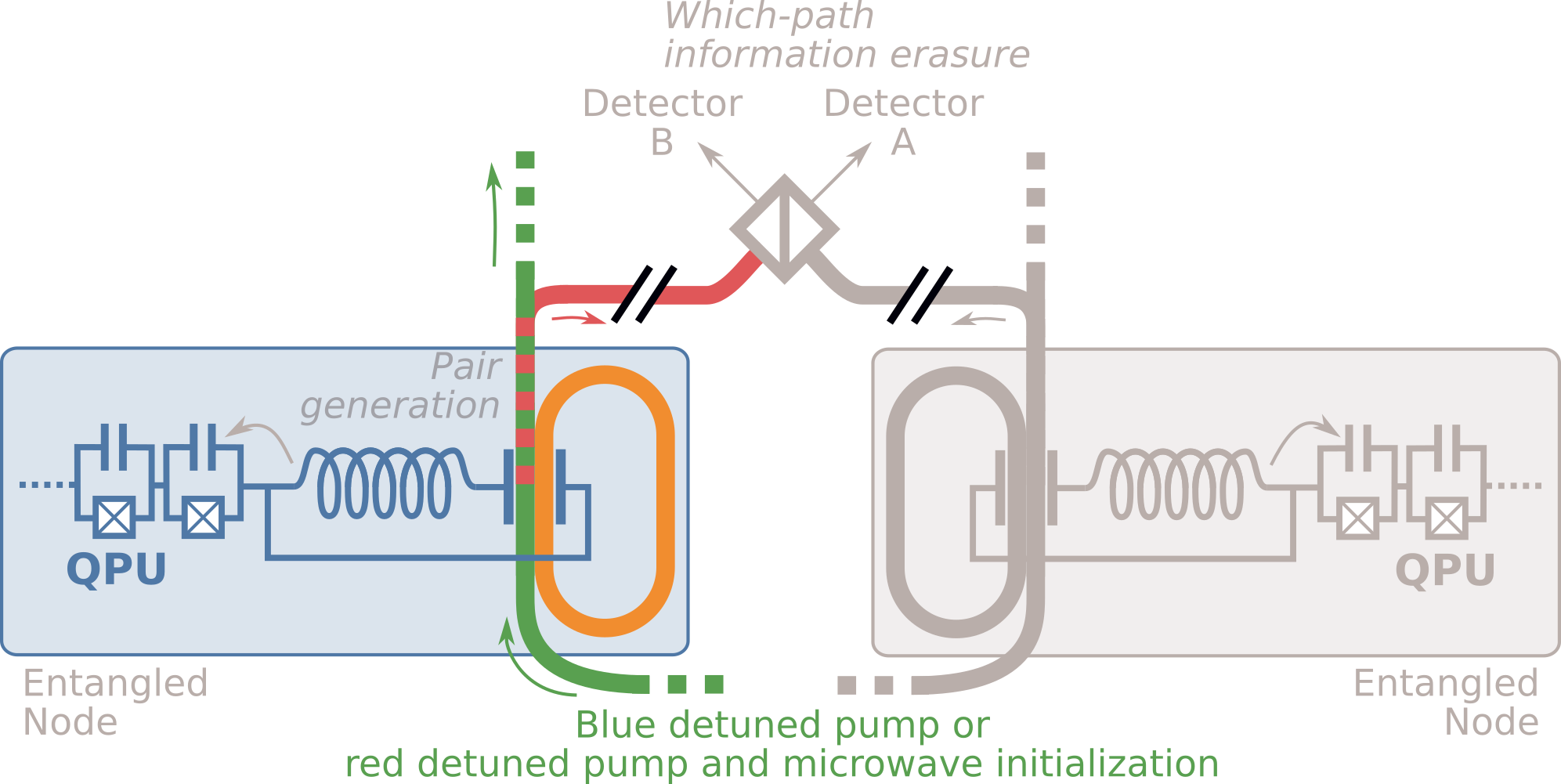
Probabilistic Heralding
  1. Krastanov et al.
    Optically Heralded Entanglement of Superconducting Systems in Quantum Networks

Rate-Fidelity tradeoff

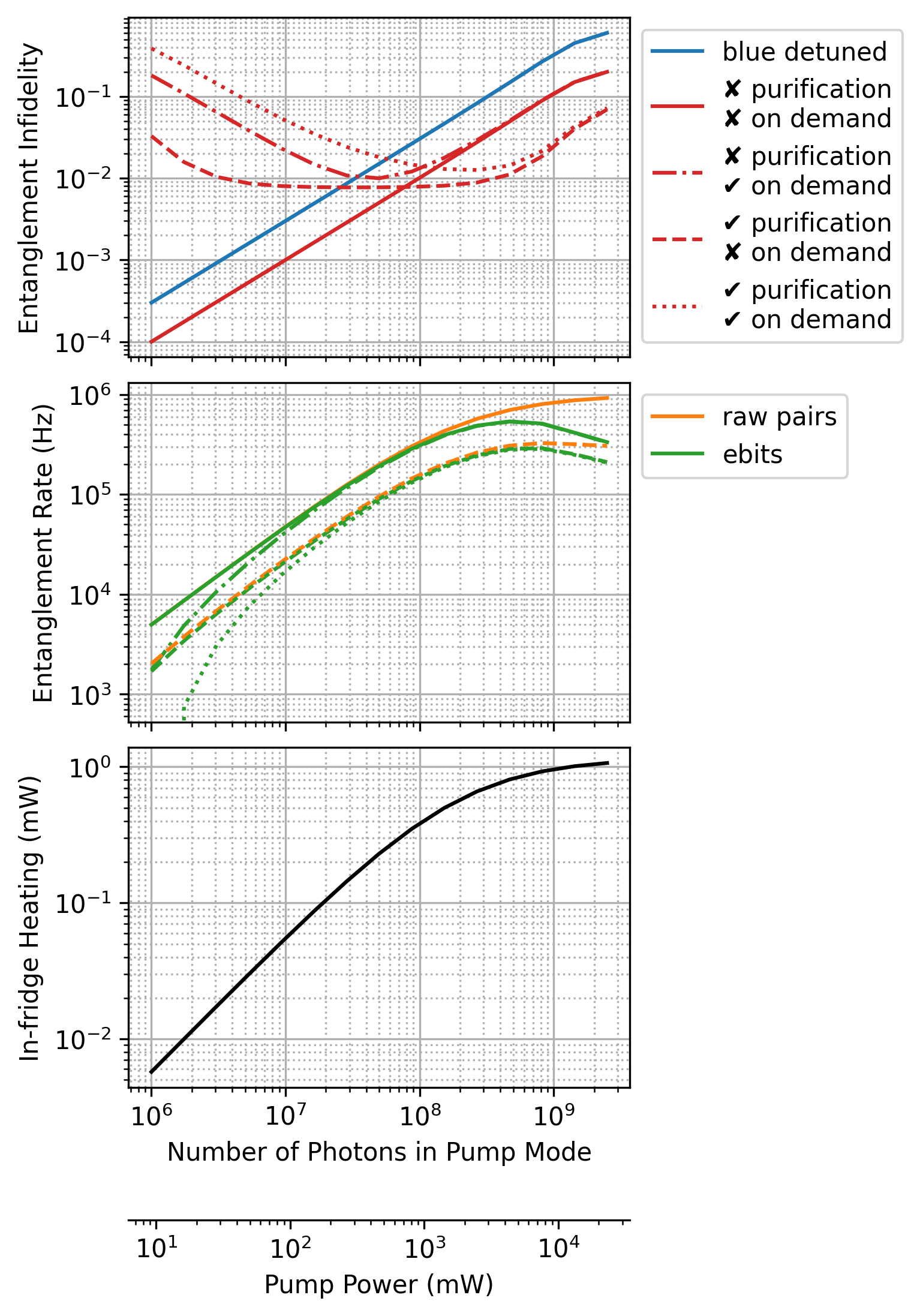
Optical to microwave for control

\(\hat{H} = g_0 \hat{a}^\dagger\hat{b}\hat{c} + \text{H.c.}\)
\(\hat{H} = g_0 \sqrt{n_a n_b}\hat{c} + \text{H.c.}\)
\(P = \gamma\hbar\omega_\text{opt}n\)
\(\frac{P}{g} \approx \frac{\gamma\hbar\omega_\text{opt}}{g_0}\)