Full-stack Quantum Hardware Design

Stefan Krastanov | UMass Amherst, MIT

U. Arizona, Harvard, MIT, Yale, BYU, U. Chicago, Howard University, U. Oregon, UMass Amherst, NAU

Computing in the Real Universe

Roman Abacus
Roman Abacus
Inca Quipo
Roman Abacus
Inca Quipo
The Analytical Engine
The Analytical Engine, envisioned by Babbage and Lovelace as a programmable computer two centuries ago¹.

What do the laws of physics permit?

$\vec{x},\vec{p}$

$\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}=\frac{\partial\mathcal{H}}{\partial\vec{p}}\ \dots$

Deterministic

P

$\vec{x},\vec{p}$

$\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}=\frac{\partial\mathcal{H}}{\partial\vec{p}}\ \dots$

Deterministic

P

$\rho\scriptstyle\left(\vec{x},\vec{p}\right)$

$\frac{\partial \rho}{\partial t}=-\left\{\rho,\mathcal{H}\right\}$

Probabilistic

BPP

$\vec{x},\vec{p}$

$\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}=\frac{\partial\mathcal{H}}{\partial\vec{p}}\ \dots$

Deterministic

P

$\rho\scriptstyle\left(\vec{x},\vec{p}\right)$

$\frac{\partial \rho}{\partial t}=-\left\{\rho,\mathcal{H}\right\}$

Probabilistic

BPP

$|\psi\rangle$

$i\hbar\frac{\mathrm{d}\ \ }{\mathrm{d} t}|\psi\rangle=\hat{H}|\psi\rangle$

Quantum

BQP

Why care about a quantum model of computation?

BQP seems bigger than P or BPP.

Useful problems become easy on a quantum device.

Going in the other direction: theoretical computer science can inform theoretical physics.

Where is the Quantum Advantage?

Computing a function on all possible inputs at the same time?

Consider searching for the zero $z$ of a function $\textrm{f}$
$\textrm{f}(z)=0$
$\textrm{f}(x)=1$ for $x\ne z$

$$ \begin{matrix} x_1 \\ x_2 \\ z \end{matrix} $$

possible inputs

$$ \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$

initial state of the computer

$$ \hat{M} \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$

executing the program

$$ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$

desired final state

$$ \begin{matrix} x_1 \\ x_2 \\ z \end{matrix} $$

possible inputs

$$ \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$

initial state of the computer

$$ \hat{M} \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$

executing the program

$$ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$

desired final state

$\hat{M}$ is "stochastic" in a probabilistic computer
$\hat{M}$ is "unitary" in a quantum computer

What about the bit?

$$ b \in \{0,1\} $$

classical bit

$$ \begin{pmatrix}p_0\\p_1\end{pmatrix} \in \mathbb{R}^2 $$ $$\scriptstyle p_0+p_1=1$$

classical probabilistic bit

$$ \begin{pmatrix}c_0\\c_1\end{pmatrix} \in \mathbb{C}^2$$ $$\scriptstyle |c_0|^2+|c_1|^2=1$$

quantum bit (qubit)

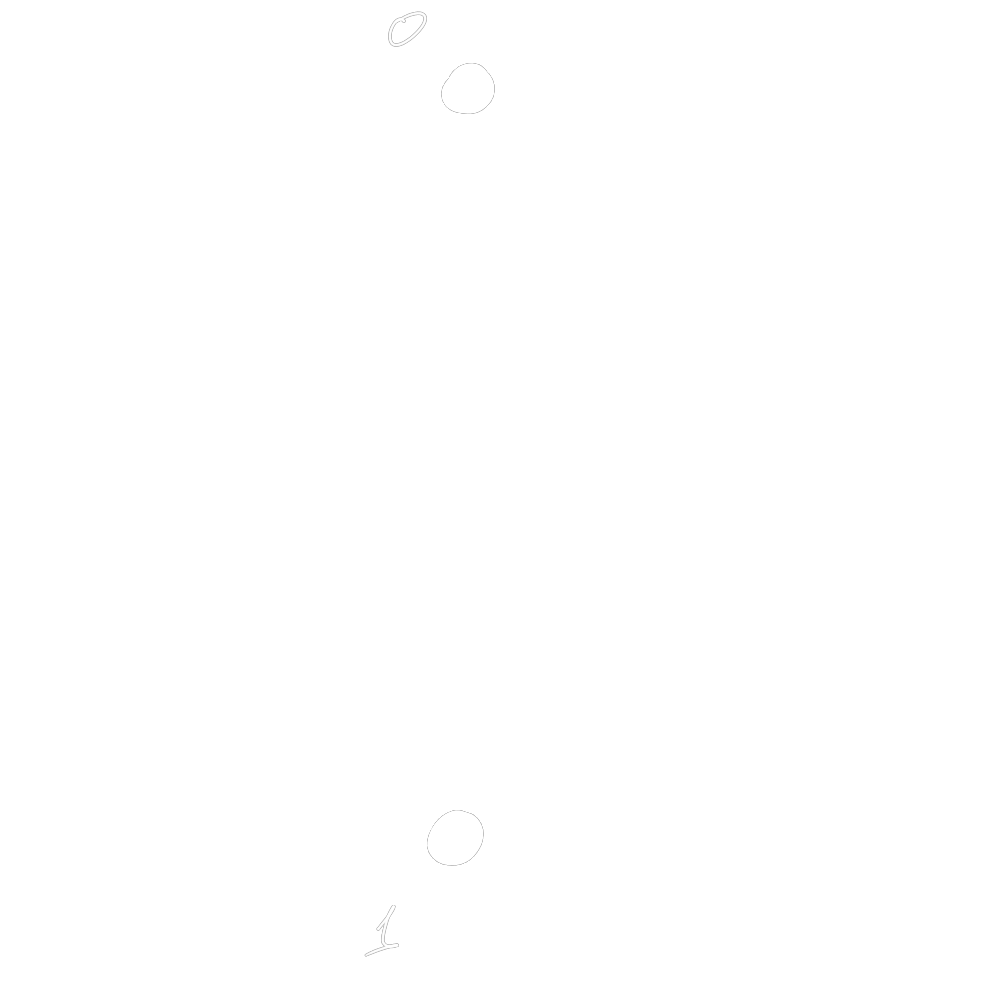
classical bit

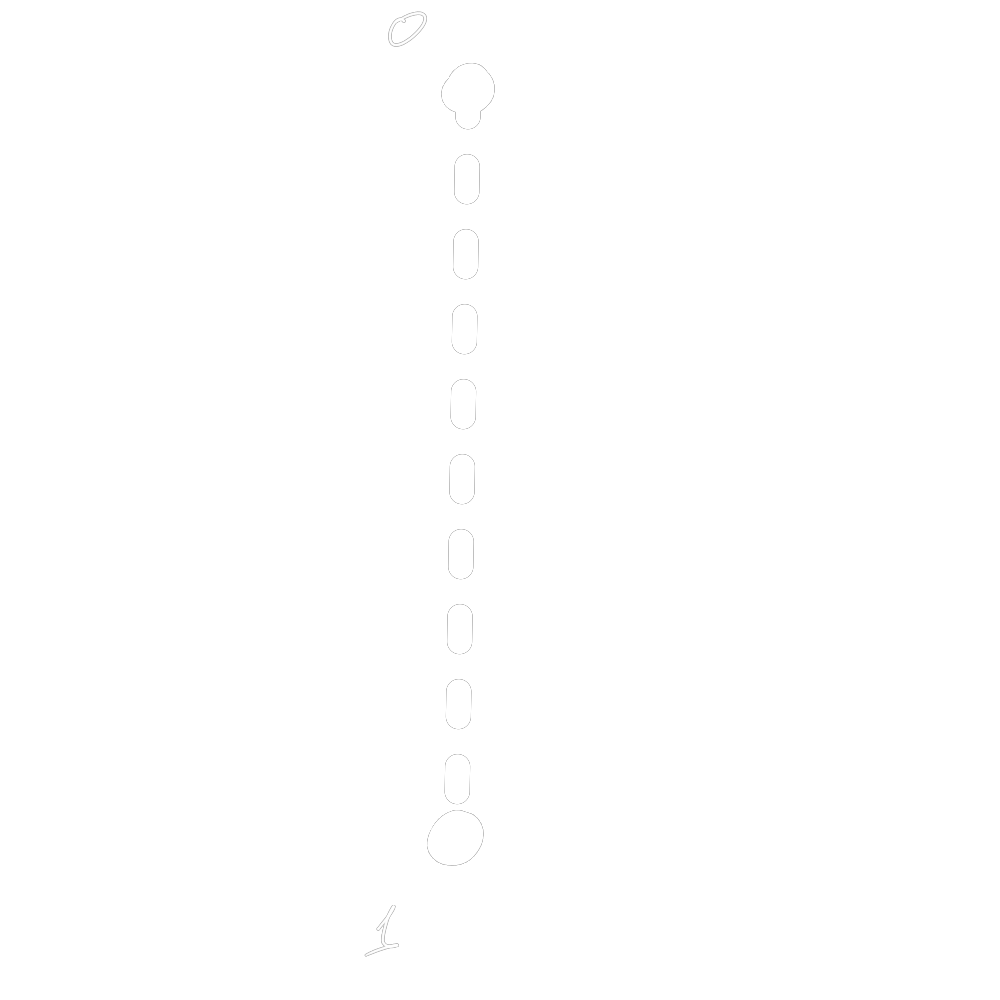
classical probabilistic bit

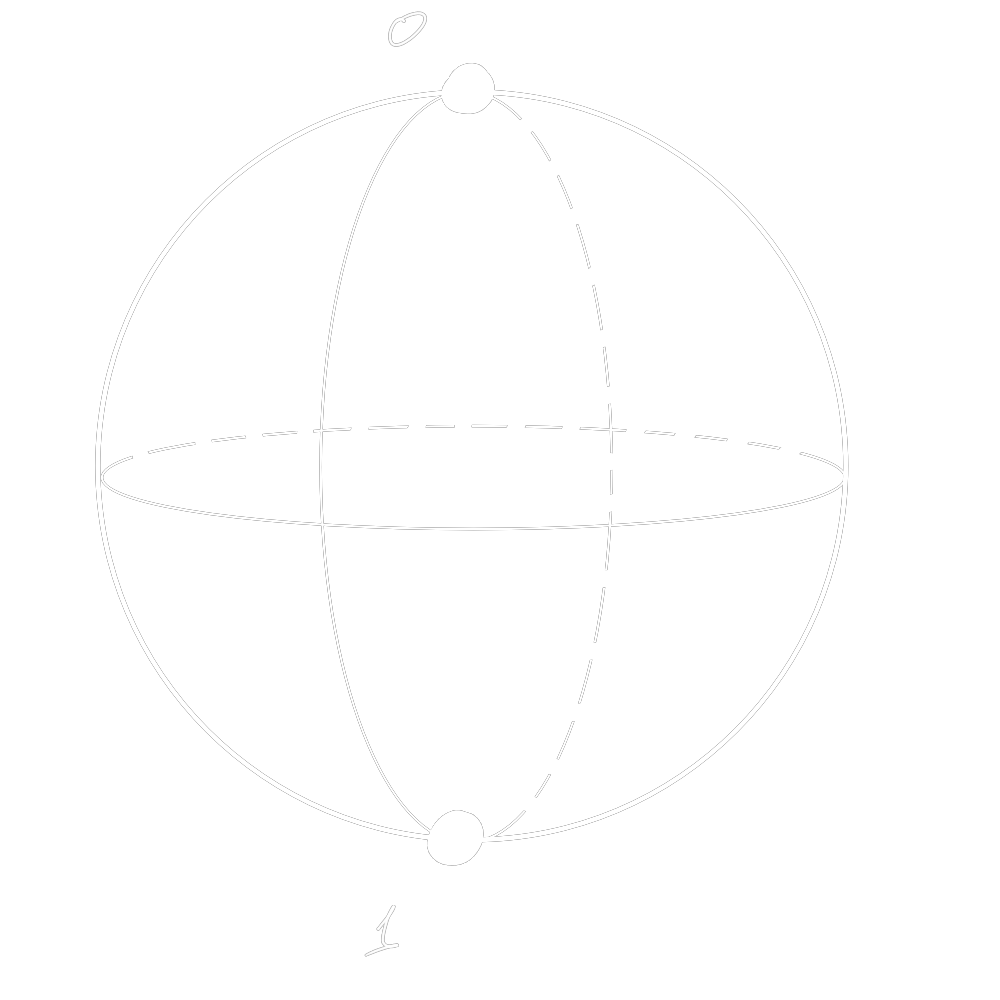
quantum bit (qubit)

Where is the Quantum Advantage?

Interference!
Sometimes the wrong results can interfere destructively!

Why is it taking so long?

The Analytical Engine, envisioned by Babbage and Lovelace as a programmable computer two centuries ago¹.
The Analytical Engine¹.

The first design for error-corrected classical computation².
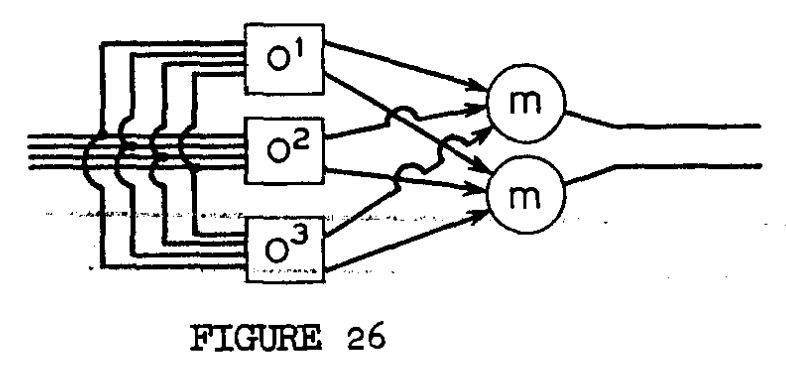
  2. von Neumann
    The Synthesis of Reliable Organisms […]
More than a hundred years between the conception of programmable machines and their realization.

  2. von Neumann
    The Synthesis of Reliable Organisms […]

The Quantum Technology Stack

Materials

Analog Control

Noisy Digital Circuits

Error Correction

Quantum Algorithms

We have the fastest "algebra of quantum error correction" tool


            a = random_pauli(1_000_000_000);
            b = random_pauli(1_000_000_000);
            @benchmark mul_left!(a,b)
            # Time  (median):     32.246 ms
1 Giga qubit ops in 32ms thanks to SIMD.jl and Polyester.jl
  1. Krastanov and contributors
    QuantumClifford.jl

... and work on GPU acceleration for error correction codes (ECC)¹

... and a library of codes and ECC circuit compilers²

... and expander-graph LDPC code generators³

Possible thanks to CUDA.jl and Nemo.jl

  1. past and current undergrad projects at MIT and Hampshire
  2. past and current undergrad projects at GSoC and UMass
  3. current undergrad projects at MIT (Vaishnavi Addala)
    QuantumExpanders.jl

And the occasional algorithmic discovery

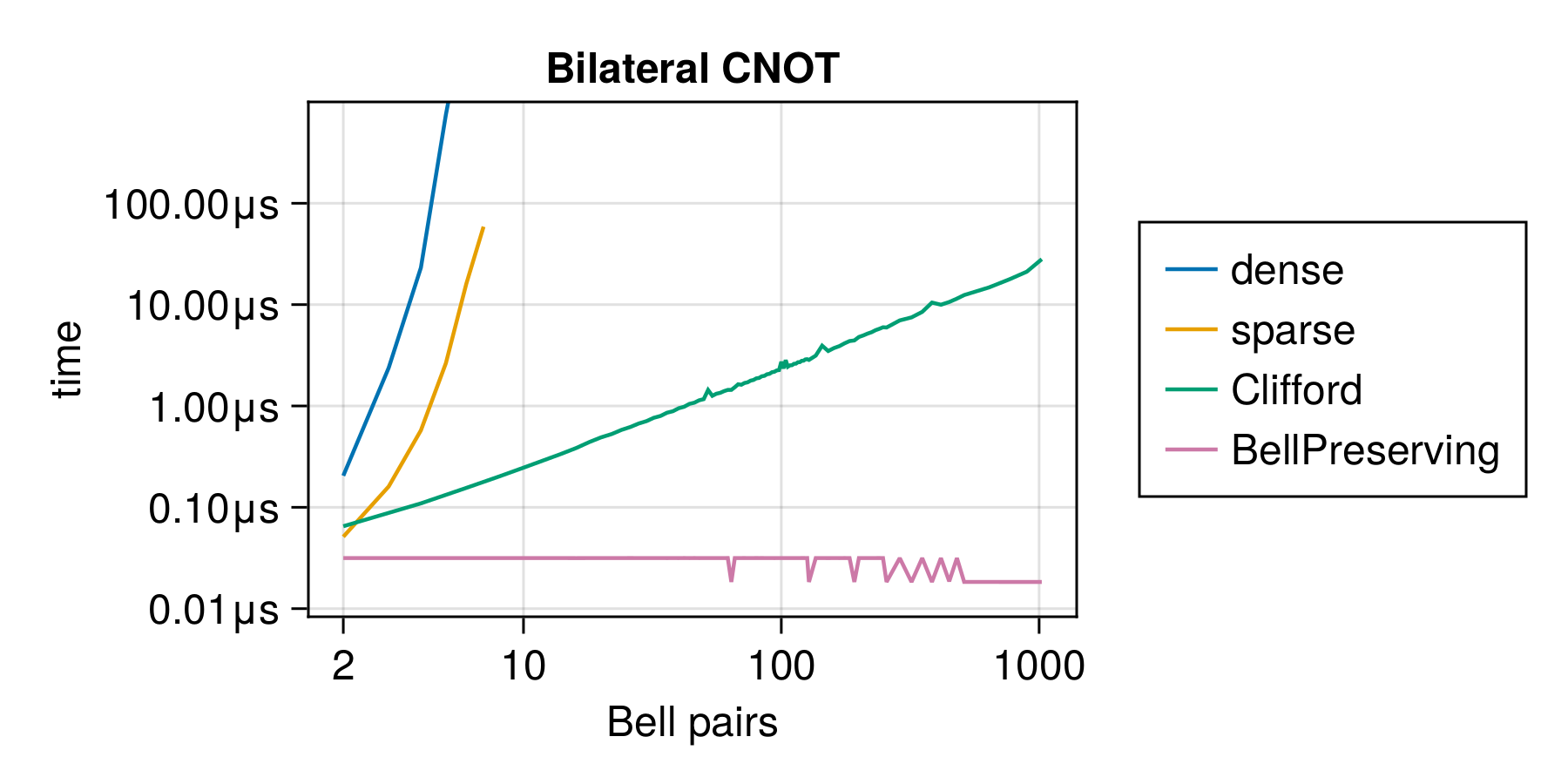
Time to perform a pair of CNOT gates, depending on formalism
  1. past undergrad projects at MIT (Shu Ge)
    BPGates.jl

The wider Julia ecosystem

QuantumOptics.jl, ITensors.jl, Yao.jl, quantum chemistry and solid state tools, EM tools, multiphisics classical tools, etc

Full-Stack Design and Optimization Toolkit

Symbolic description of quantum logic

Declarative noise models

Translation to many simulator backends

Discrete event scheduler

High-level lego-like interface

Symbolic description of quantum logic


              julia> X1⊗L1
              |+⟩|1⟩
              
              julia> express(X1⊗L1)
              Ket(...) # a dense vector from
                       # QuantumOptics.jl

              julia> express(X1⊗L1, CliffordRepr())
                X_    # an exponentially more-efficient
               -_Z    # representation from
                      # QuantumClifford.jl
Build upon Symbolics.jl and many "backend" library. 

                traits = [Qubit(), Qubit(), Qumode()]
                reg = Register(traits)

A register "stores" the states being simulated.

Translation to many simulator backends


                initialize!(reg[1], X₁)

A register's slot can be initialized to an arbitrary state, e.g. $|x_1\rangle$ an eigenstate of $\hat{\sigma}_x$.

Translation to many simulator backends


                initialize!(reg[1], X₁)
                initialize!(reg[2], Z₁)
                apply!((reg[1], reg[2]), CNOT)

Arbitrary quantum gates or channels can be applied.

Translation to many simulator backends


                initialize!(reg[1], X₁)
                initialize!(reg[2], Z₁)
                apply!((reg[1], reg[2]), CNOT)

Arbitrary quantum gates or channels can be applied.

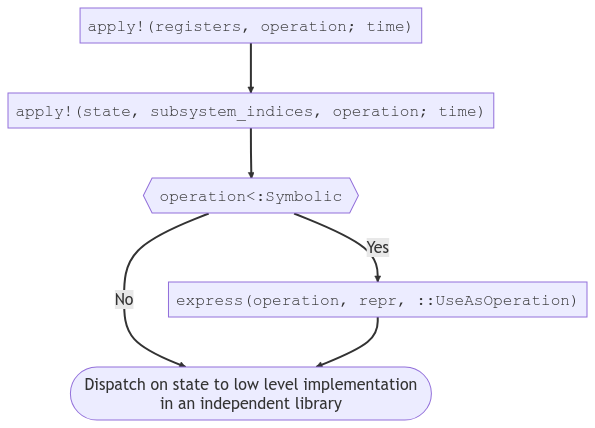
Discrete event scheduler

Locks and channels, message passing, delays, concurrency, agent-based sims...

Discrete event scheduler

High-level lego-like interface

Full repeater sim with automatic instrumentation.

QuantumSavory.jl

github.com/Krastanov/QuantumSavory.jl

prerelease...

We are hiring both at UMass Amherst and MIT:
software engineering
quantum science

Message at stefankr@mit.edu, skrastanov@umass.edu

 

Including work done by Vaishnavi Addala and Shu Ge, in coordination with Dirk Englund.

Consider gradschool or postdoc at UMass Amherst:

Design of optical/mechanical/spin devices with Sandia, Mitre, and MIT.

Working on practical LDPC ECC in networking and computing with CQN.

Creating new tools for the entire community.