Digital Twins for Quantum Hardware: Multi-formalism and Mixed-signal
Stefan Krastanov | MIT ⟶ UMass AmherstThe Quantum Technology Stack
Materials
Analog Control
Noisy Digital Circuits
Error Correction
Quantum Algorithms
Analog Quantum Hardware
Room-Temperature Optical Quantum Computing
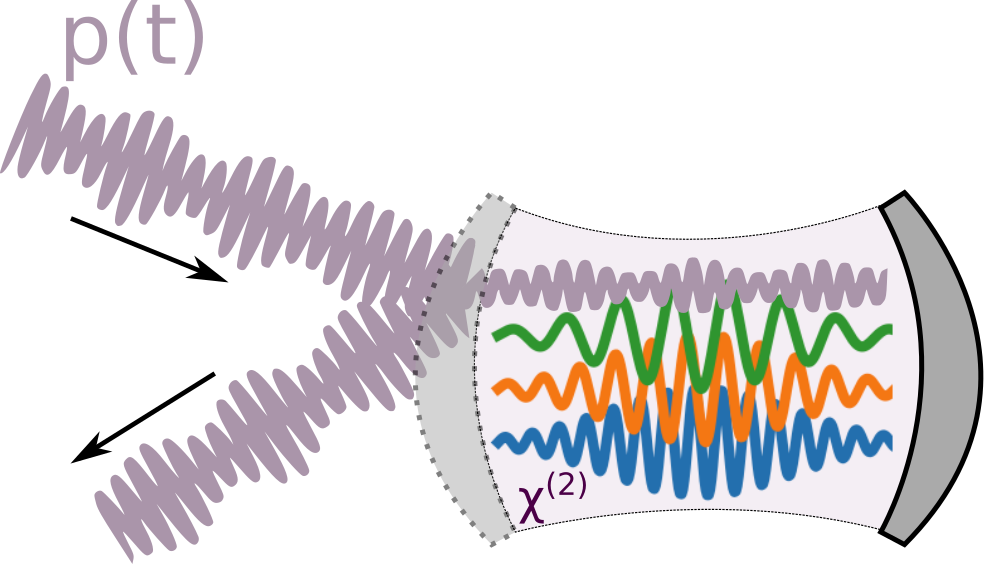
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities

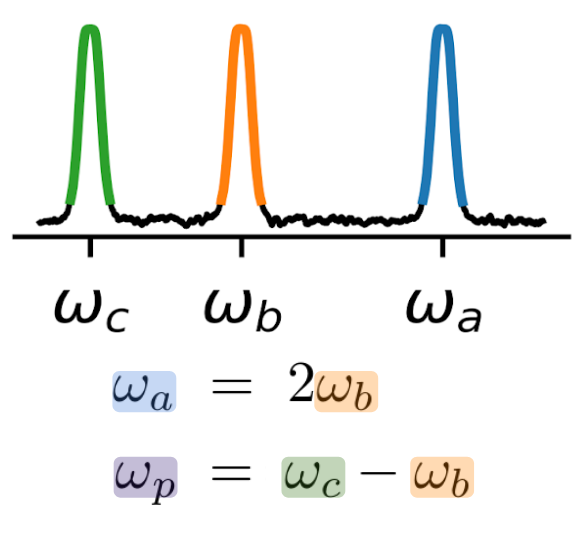
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities


- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities


A rather "poor" Hamiltonian...
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
Can be twisted into something useful:
Can be twisted into something useful:
Full error correction
Can be twisted into something useful:
Full error correction
Can be twisted into something useful:
Full error correction

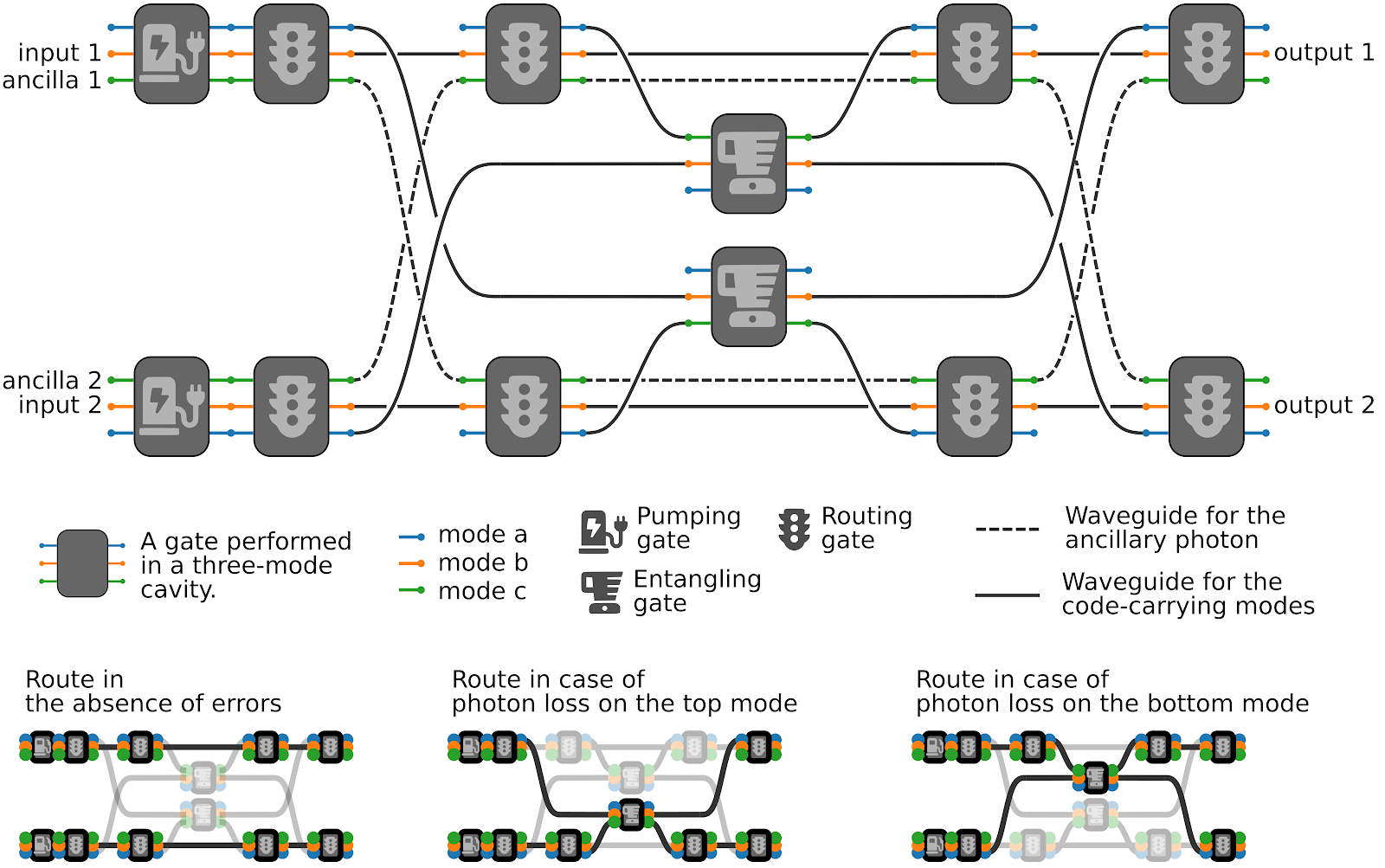
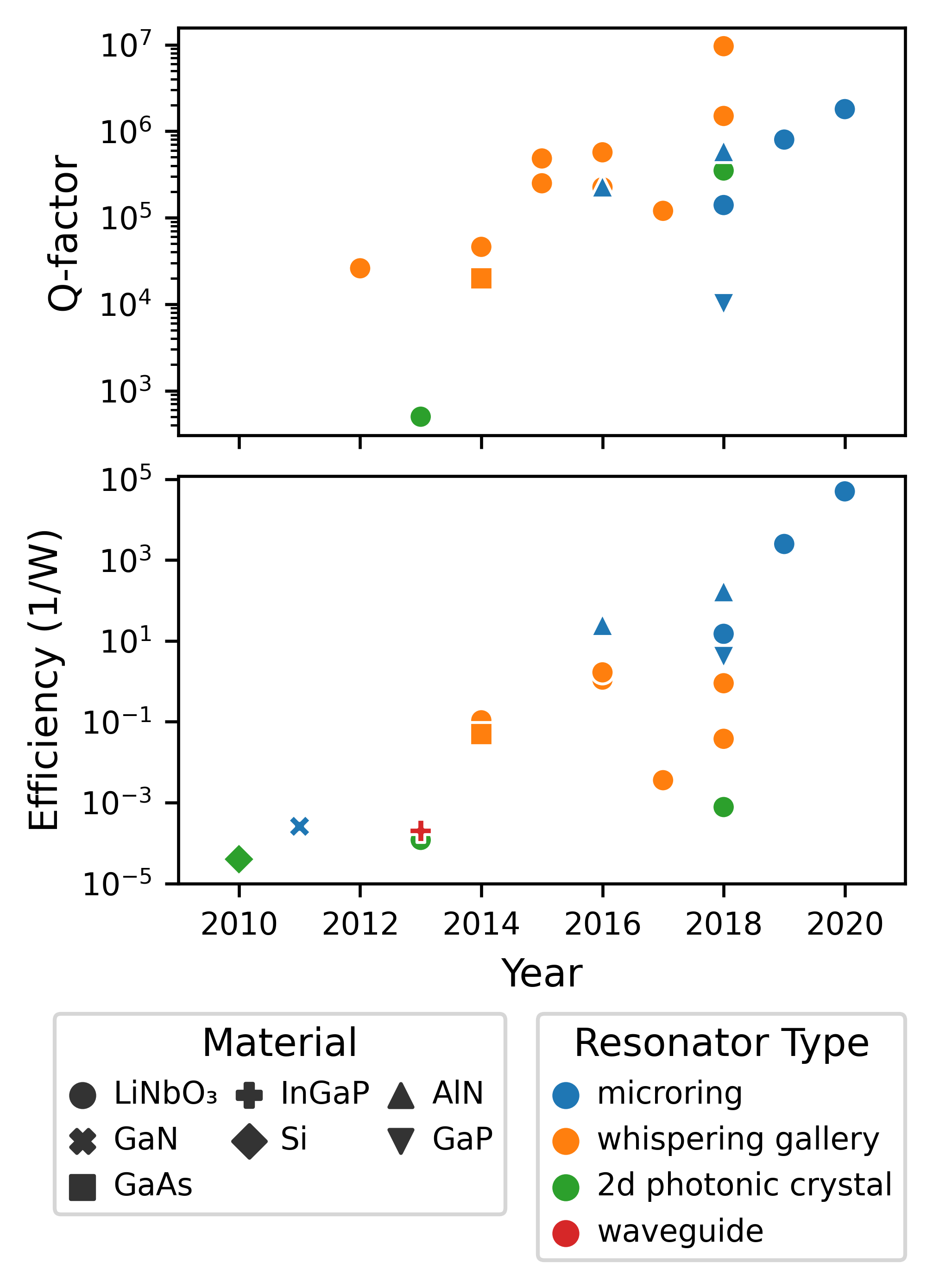
Is this a realistic device?
Similar design work
Similar design work

- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani, …, KrastanovAll-Photonic Artificial Neural Network Processor Via Non-linear Optics
Similar design work

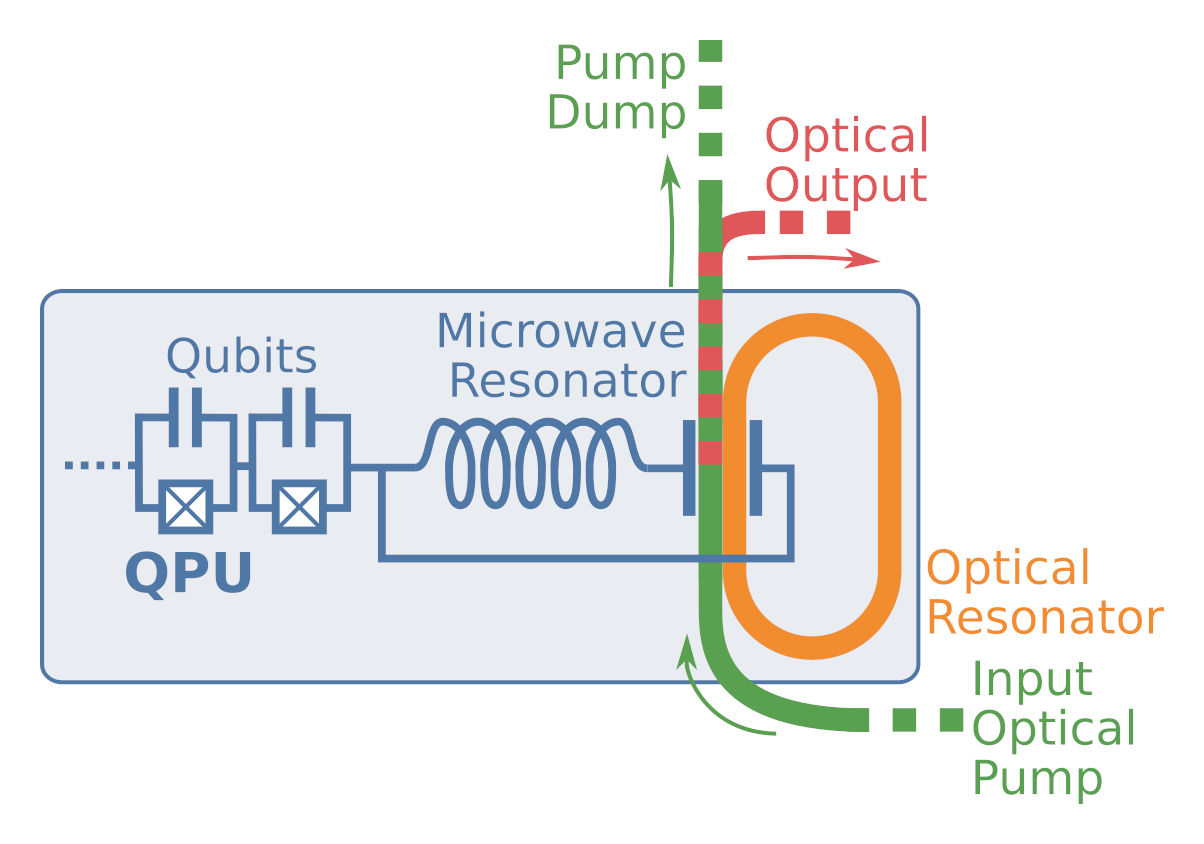
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani, …, KrastanovAll-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks
Similar design work


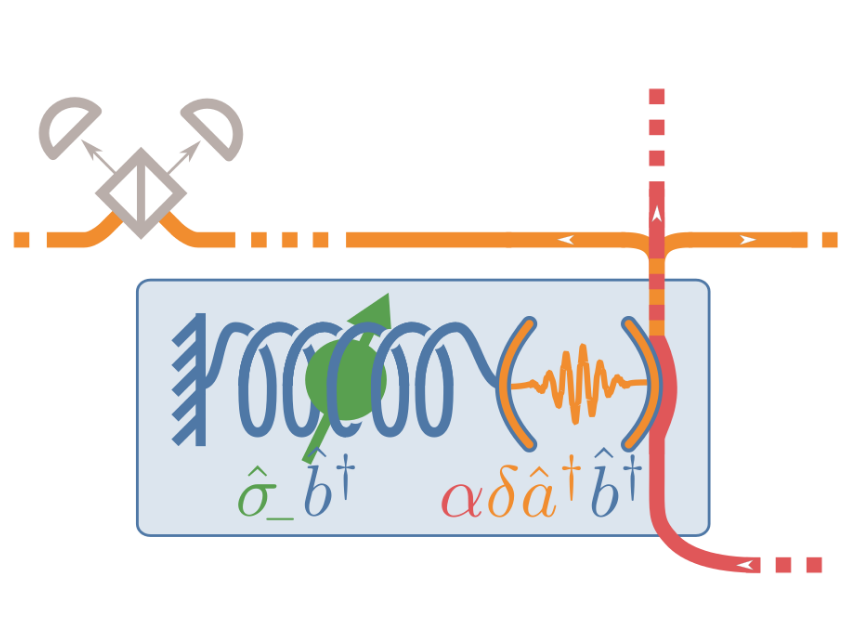
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani, …, KrastanovAll-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks
- Raniwala*, Krastanov* et al.A spin-optomechanical quantum interface [...]
Better Tools for these Analog Control Problems

- Krastanov et al.Unboxing Quantum Black Box Models [...]
- Krastanov et al.Stochastic estimation of dynamical variables
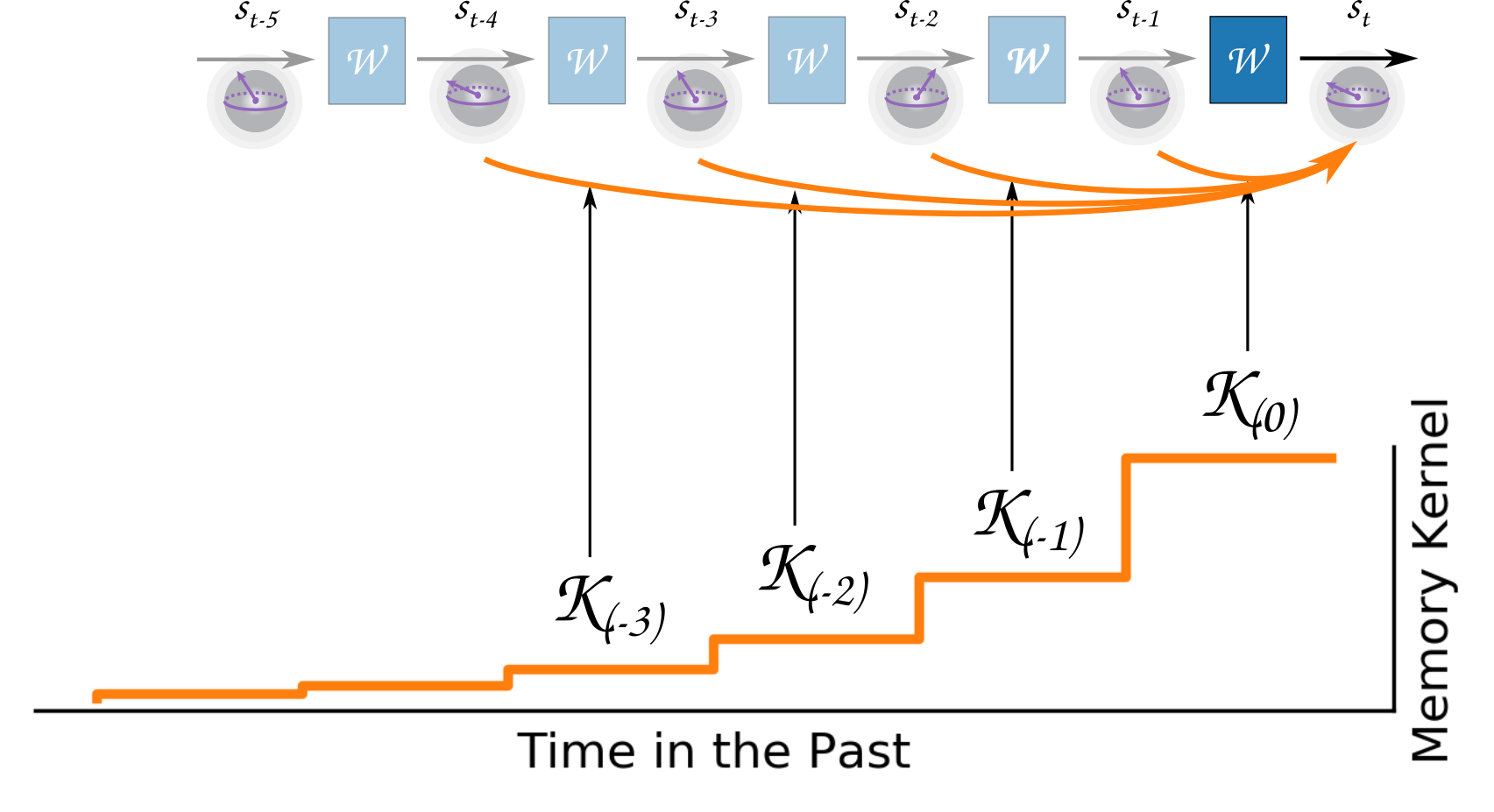
\(\frac{\mathrm{d}\rho}{\mathrm{d}t}= -i\left[H,\rho(t)\right]+\int_0^t\mathcal{K}(\tau)\mathcal{D}\left(L,\rho(t-\tau)\right)\mathrm{d}\tau\)
- Krastanov et al.Unboxing Quantum Black Box Models [...]
Less Pretentious Version of the Same Statement
Use automatic differentiation and stochastic gradient descent more, you will be surprised by the high quality of the results.
Digital Quantum Hardware
or "Quantum Supremacy"
Noisy Clifford Circuits
Purification of entanglement
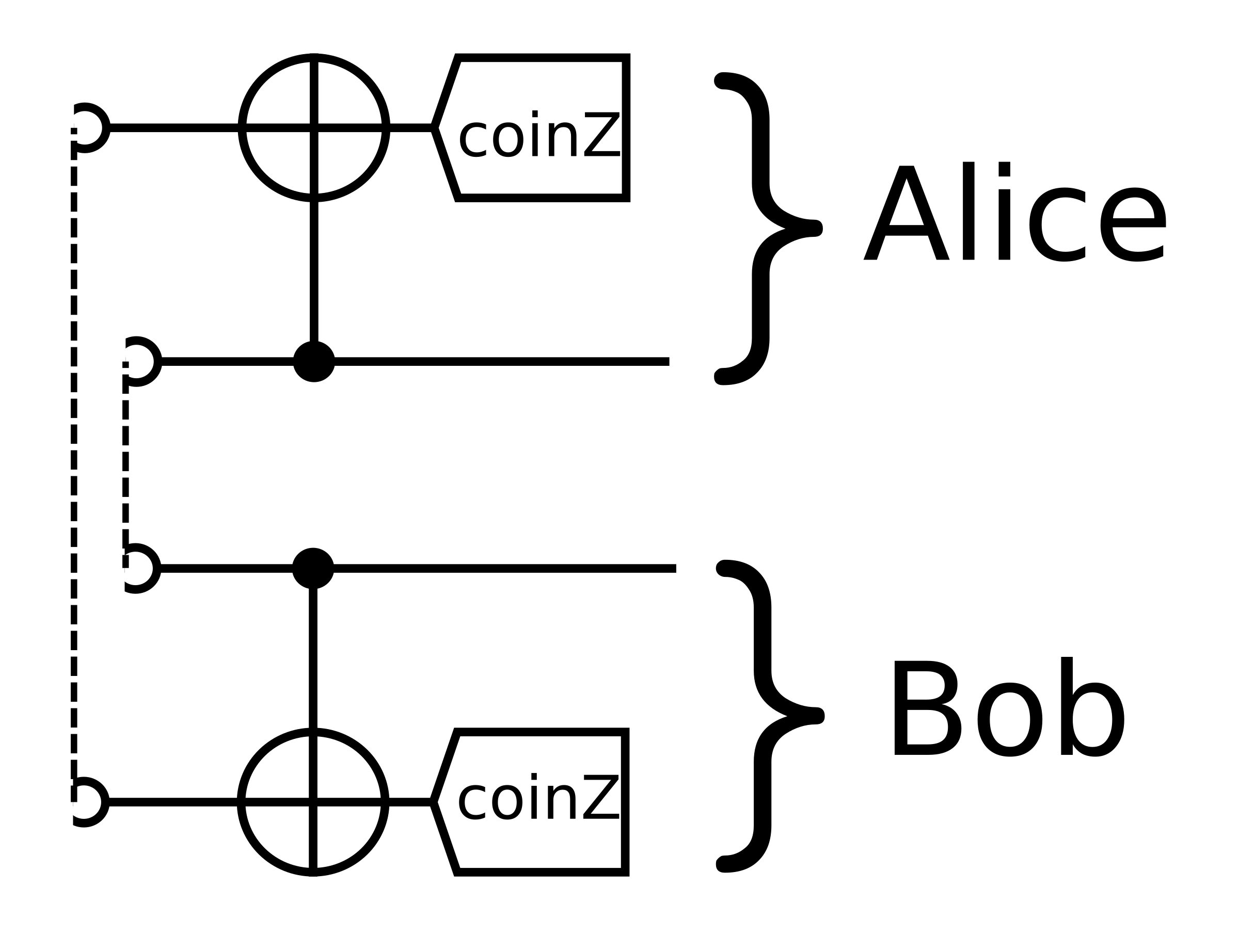
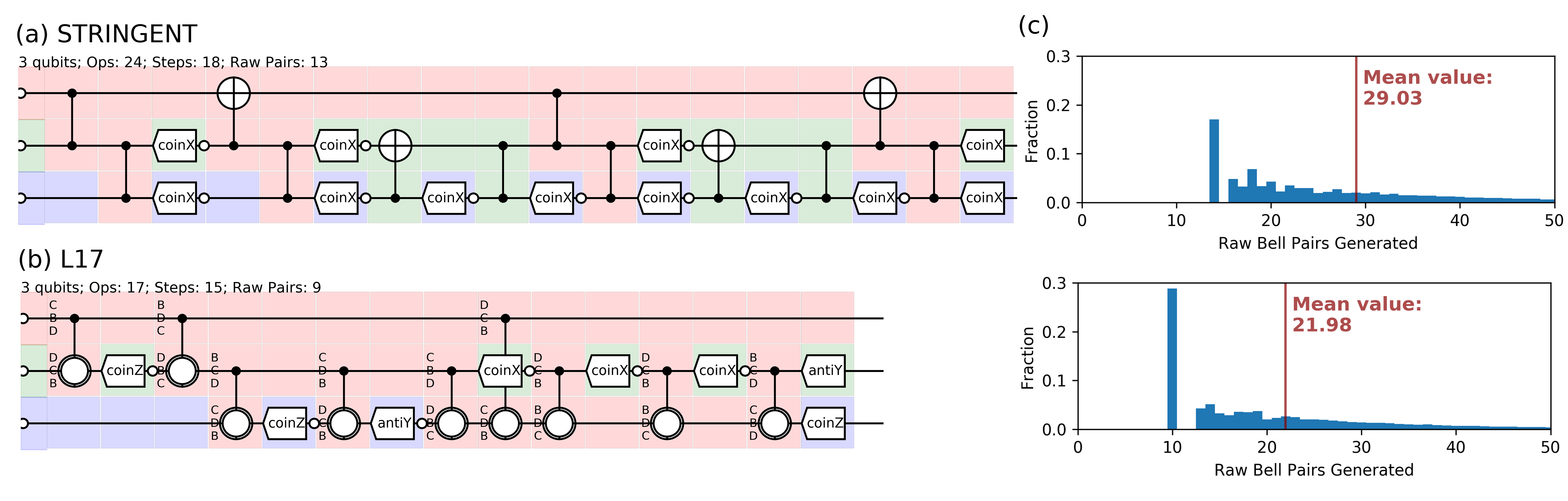
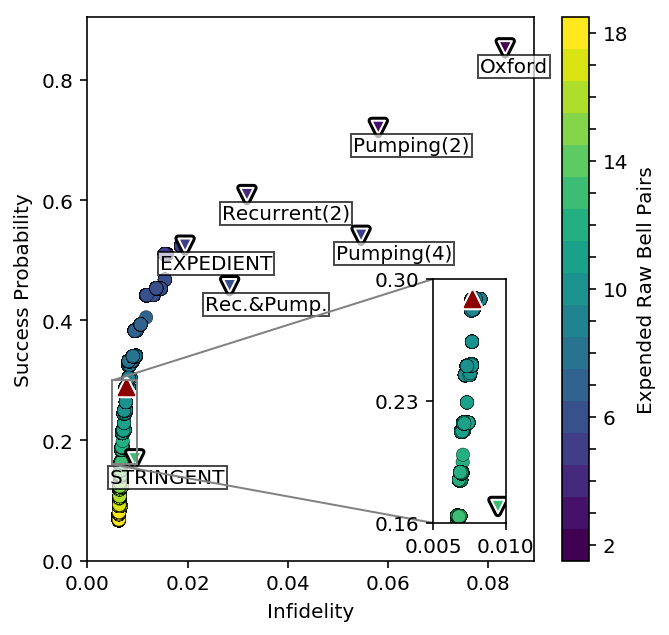
Optimized circuits for purification¹, better than any known circuits.
- Krastanov et al.Optimized Entanglement Purification

Optimized circuits for purification¹, better than any known circuits.
Turns out they are also "the best" after exhaustive comparision².
- Krastanov et al.Optimized Entanglement Purification
- Jansen et al. @ DelftEnumerating all bilocal Clifford distillation protocols through symmetry reduction
Ongoing work
n-to-k purification circuits¹
Assymptotically faster simulations of purification circuits²
- Delft and MIT friends
- Ge, KrastanovSimulating Entangled States and Purification Circuits Faster than the Stabilizer Tableaux Formalism
Generating Good Error Correcting Codes
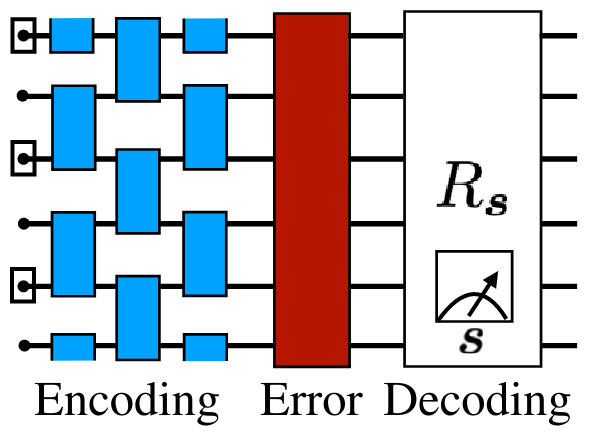
Fast evaluation of Clifford Circuits helps with the design of error correction codes¹
- Gullans et al.Quantum Coding with Low-Depth Random Circuits
Tools: Simulators for Noisy Clifford Circuits
QuantumClifford.jl
- Tableau Algebra
- Random Cliffords
- Destabilizers
- Symbolic
- Fast
Tools: QuantumClifford.jl is fast
julia> a = random_pauli(1_000_000_000);
julia> b = random_pauli(1_000_000_000);
julia> @benchmark QuantumClifford.mul_left!(a,b)
Time (median): 32.246 ms
Tools: QuantumClifford.jl lets you study symbolic structure
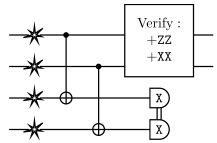
A noisy purification circuit
g1 = sCNOT(1,3)
g2 = sCNOT(2,4)
m = BellMeasurement(...)
v = VerifyOp(...)
n = NoiseOpAll(epsilon)
failure = 4e*((1 - 3e)^3)
false_success = 6e*((1 - 3e)^3)
true_success = (1 - 3e)^4 + ...
Tools: Ongoing work
GPU accelerated Clifford Circuits¹
Code libraries²
- El Dandachi, Krastanov
- Garcés, Krastanov
Full-Stack Design and Optimization Toolkit
Types of Dynamics
Types of Dynamics
Hamiltonians, Master Equations
Types of Dynamics

Hamiltonians, Master Equations

Gates, Circuits
Types of Dynamics

Hamiltonians, Master Equations

Gates, Circuits
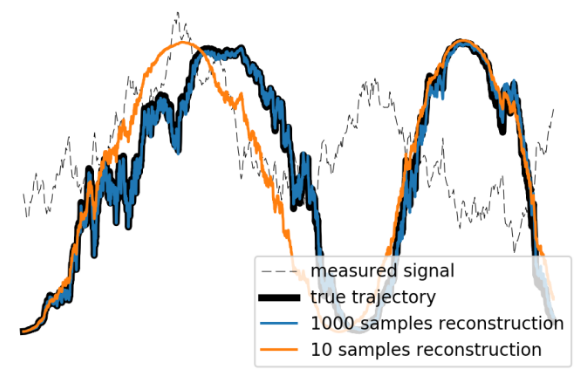
Weak Measurements, Feedback
State Representation
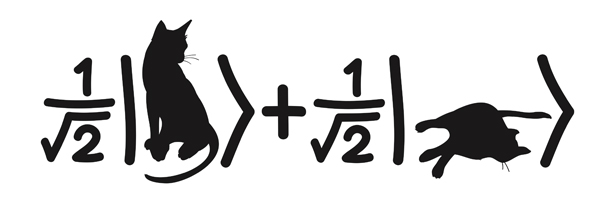

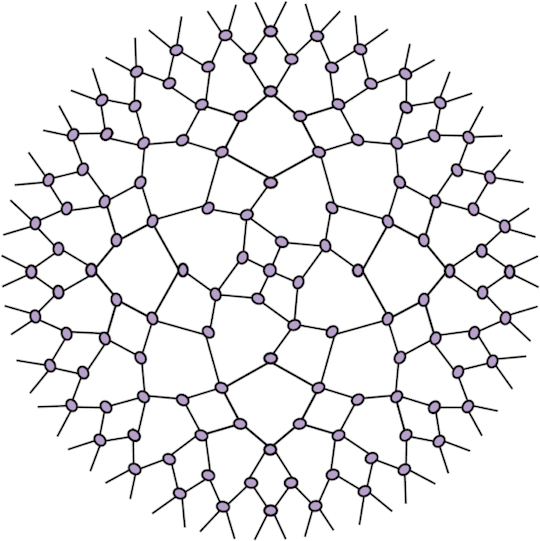
Continuous evolution at one layer, followed by noisy Clifford circuit simulator...
... and discrete event simulators
... and support for symbolic algebra systems
... running on computational accelerators like GPUs
... support for other formalisms
... all of this, with auto-differentiation and reverse design
QuantumSavory.jl
QuantumSavory.jl


QuantumSavory.jl


QuantumSavory.jlQuantumSavory.jl

QuantumSavory.jl: A tool for analog and digital quantum hardware design.Automatic tracking of noise processes

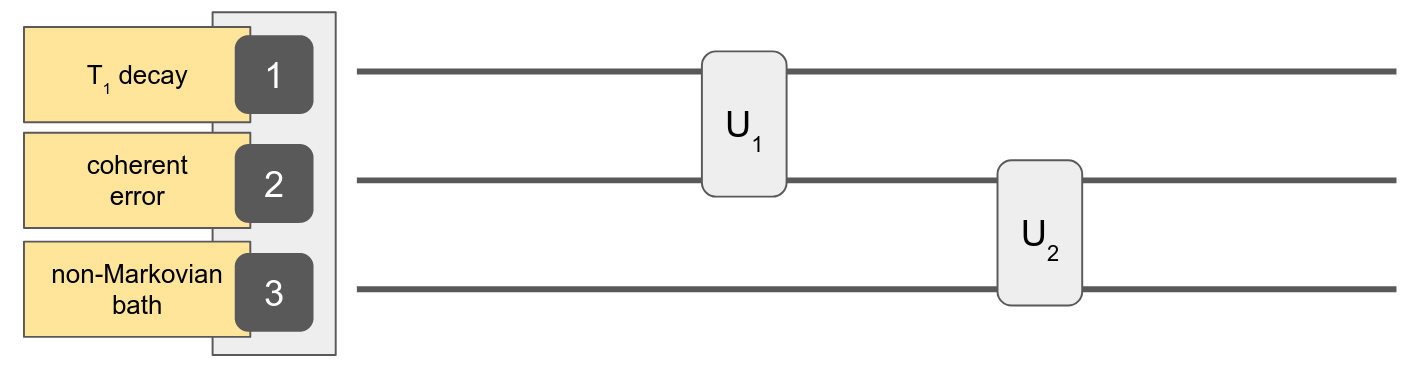
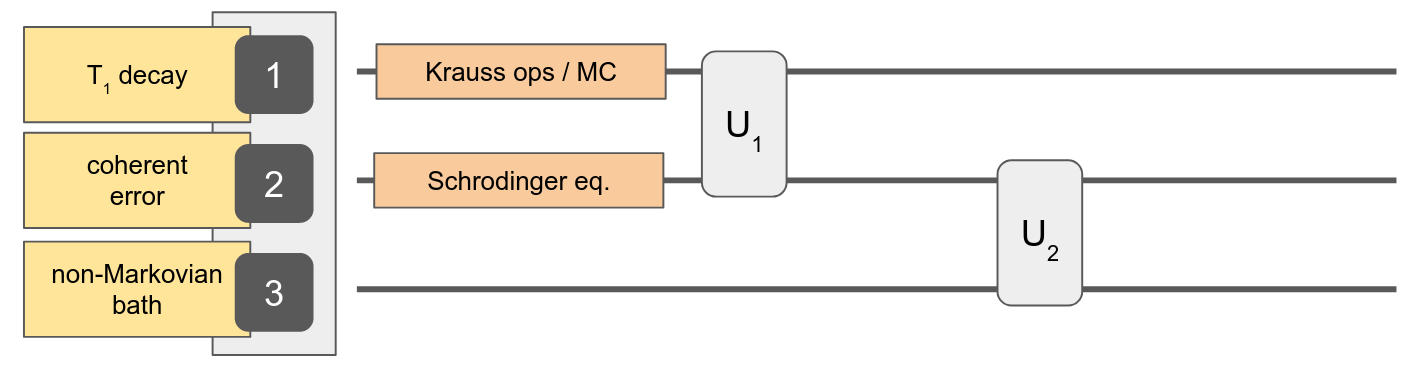
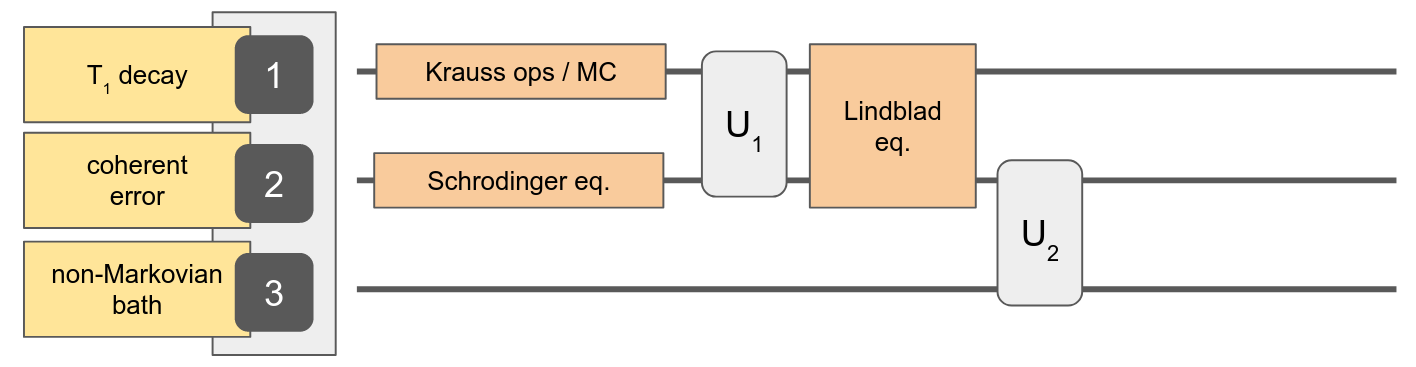
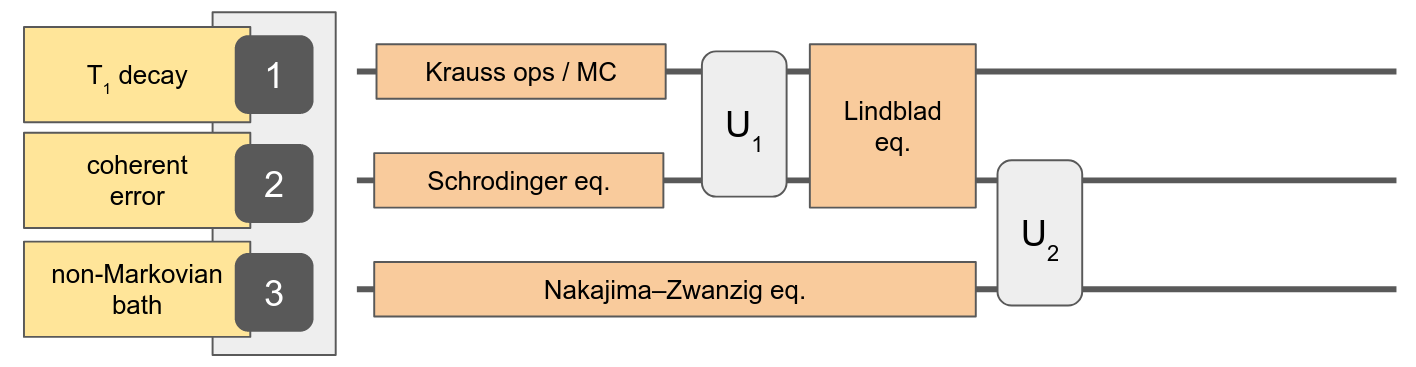
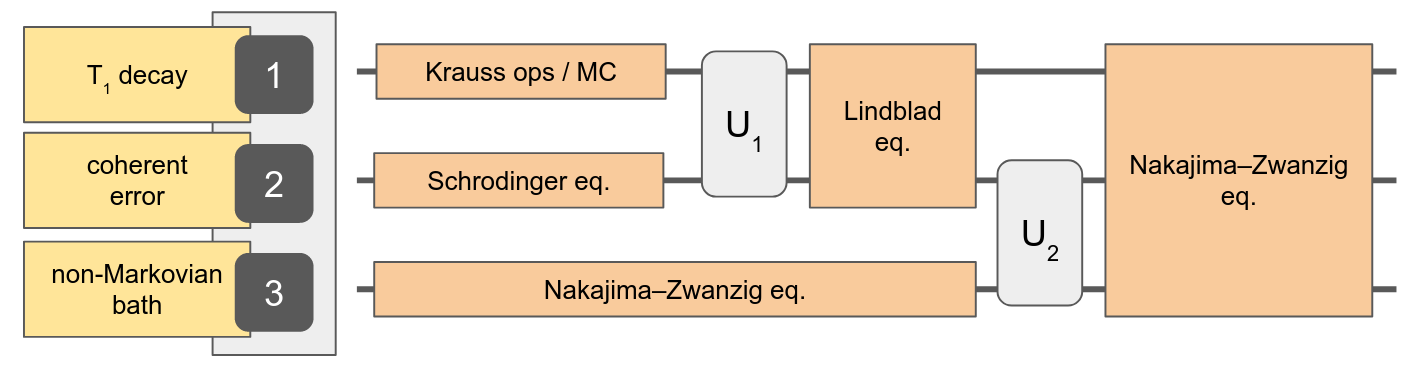
Automatic conversion between representations
Int * Float ⟶ Float
Ket ⊗ Density Matrix ⟶ Density Matrix
Ket ⊗ Tableau ⟶ Ket
Ket ⊗ Tableau ⟶ Twirled Density Matrix ???
First-gen Quantum Repeater Example
for (;src, dst) in edges(mgraph)
@process entangler(sim, mgraph, src, dst, ...)
end
for (;src, dst) in edges(mgraph)
@process entangler(sim, mgraph, src, dst, ...)
end
for node in vertices(mgraph)
@process swapper(sim, mgraph, node, ...)
end
for (;src, dst) in all_node_pairs(mgraph)
@process entangler(sim, mgraph, src, dst, ...)
end

- Dong et al.High-speed programmable photonic circuits in a cryogenically compatible, visible–near-infrared 200 mm CMOS architecture
low-level hardware control,
resource purification,
optimization of error-correcting codes,
quantum network protocols,
and generally co-design across the layers of the technology stack.
Try out QuantumClifford.jl - it is public and stable
Be an early tester for QuantumSavory.jl
Consider a postdoc at UMass Amherst:

Design of optical/mechanical/spin devices with Sandia, Mitre, and MIT.
Creating new tools for the entire community.