Full-stack Quantum Hardware Design
Stefan Krastanov | MITComputing in the Real Universe







What do the laws of physics permit?
$\vec{x},\vec{p}$
$\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}=\frac{\partial\mathcal{H}}{\partial\vec{p}}\ \dots$
P
$\vec{x},\vec{p}$
$\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}=\frac{\partial\mathcal{H}}{\partial\vec{p}}\ \dots$
P
$\rho\scriptstyle\left(\vec{x},\vec{p}\right)$
$\frac{\partial \rho}{\partial t}=-\left\{\rho,\mathcal{H}\right\}$
BPP
$\vec{x},\vec{p}$
$\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}=\frac{\partial\mathcal{H}}{\partial\vec{p}}\ \dots$
P
$\rho\scriptstyle\left(\vec{x},\vec{p}\right)$
$\frac{\partial \rho}{\partial t}=-\left\{\rho,\mathcal{H}\right\}$
BPP
$|\psi\rangle$
$i\hbar\frac{\mathrm{d}\ \ }{\mathrm{d} t}|\psi\rangle=\hat{H}|\psi\rangle$
BQP
Why care about a quantum model of computation?
BQP seems bigger than P or BPP.
Useful problems become easy on a quantum device.
Going in the other direction: theoretical computer science can inform theoretical physics.
Where is the Quantum Advantage?
Computing a function on all possible inputs at the same time?
Consider searching for the zero $z$ of a function $\textrm{f}$
$\textrm{f}(z)=0$
$\textrm{f}(x)=1$ for $x\ne z$
$$ \begin{matrix} x_1 \\ x_2 \\ z \end{matrix} $$
possible inputs
$$ \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$
initial state of the computer
$$ \hat{M} \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$
executing the program
$$ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$
desired final state
$$ \begin{matrix} x_1 \\ x_2 \\ z \end{matrix} $$
possible inputs
$$ \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$
initial state of the computer
$$ \hat{M} \begin{pmatrix} p_{x_1} \\ p_{x_2} \\ p_{z} \end{pmatrix} $$
executing the program
$$ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$
desired final state
What about the bit?
$$ b \in \{0,1\} $$
classical bit
$$ \begin{pmatrix}p_0\\p_1\end{pmatrix} \in \mathbb{R}^2 $$ $$\scriptstyle p_0+p_1=1$$
classical probabilistic bit
$$ \begin{pmatrix}c_0\\c_1\end{pmatrix} \in \mathbb{C}^2$$ $$\scriptstyle |c_0|^2+|c_1|^2=1$$
quantum bit (qubit)
classical bit

classical probabilistic bit
quantum bit (qubit)
Where is the Quantum Advantage?


Why is it taking so long?



- von NeumannThe Synthesis of Reliable Organisms […]


- von NeumannThe Synthesis of Reliable Organisms […]
The Quantum Technology Stack
Materials
Analog Control
Noisy Digital Circuits
Error Correction
Quantum Algorithms
Analog Quantum Hardware
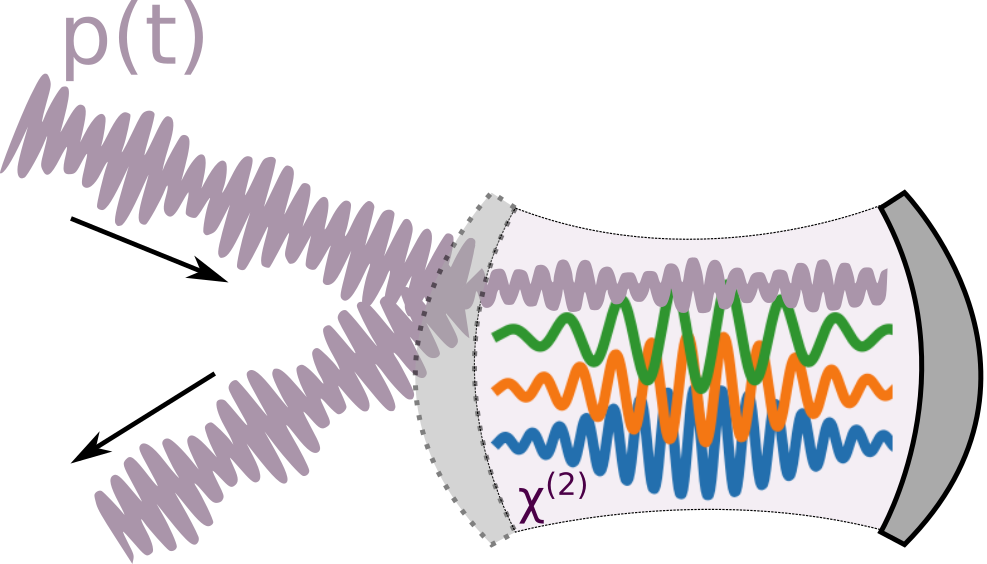
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities

- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
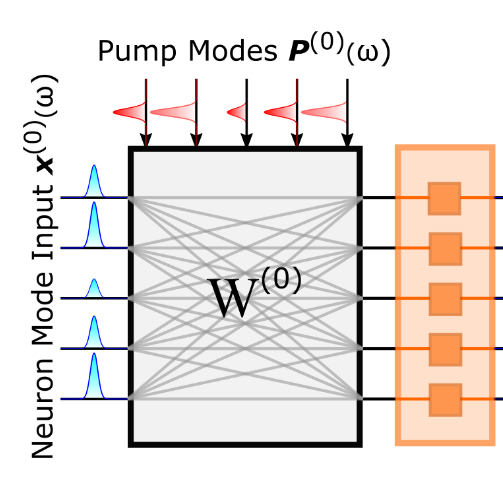
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics



- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks



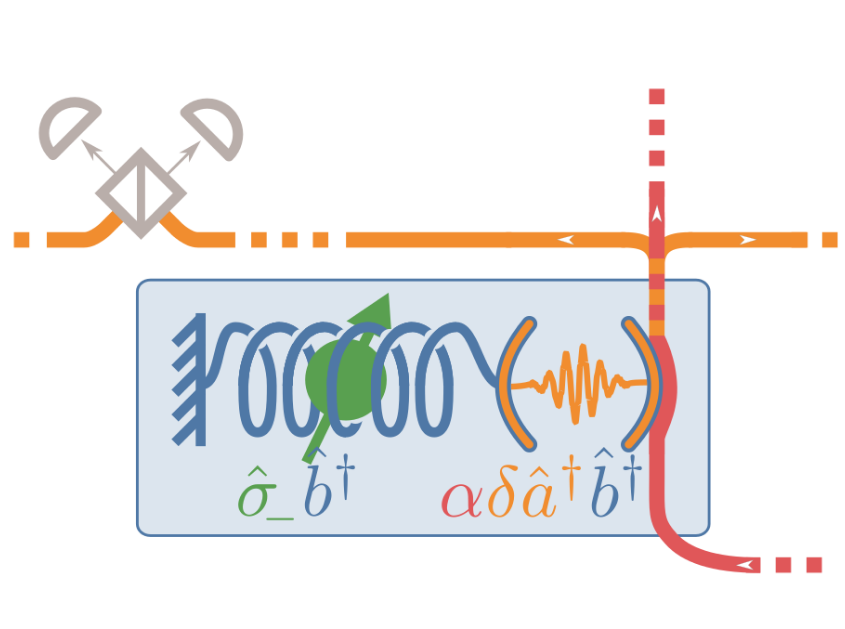
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks
- Raniwala*, Krastanov* et al.A spin-optomechanical quantum interface [...]




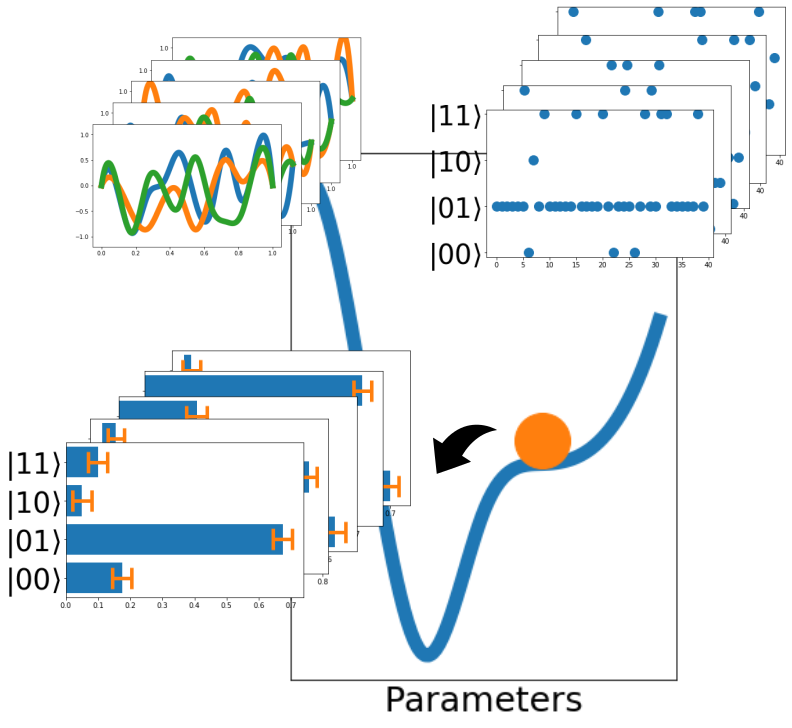
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks
- Raniwala*, Krastanov* et al.A spin-optomechanical quantum interface [...]
- Krastanov et al.Stochastic estimation of dynamical variables
- Krastanov et al.Unboxing Quantum Black Box Models [...]
Analog Quantum Hardware
Room-Temperature Optical Quantum Computing

- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities

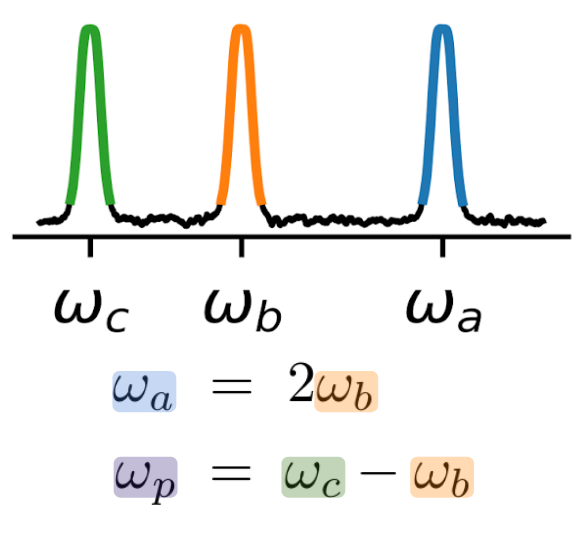
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities


- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities


A rather "poor" Hamiltonian...
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
Can be twisted into something useful:
Can be twisted into something useful:
Full error correction
Can be twisted into something useful:
Full error correction
Can be twisted into something useful:
Full error correction
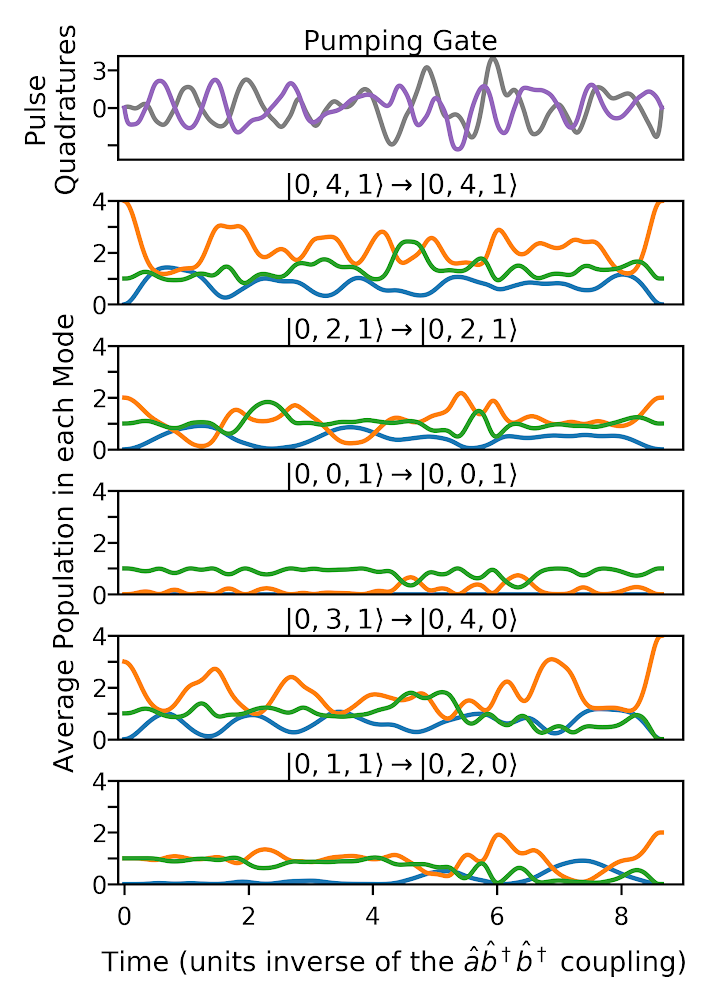
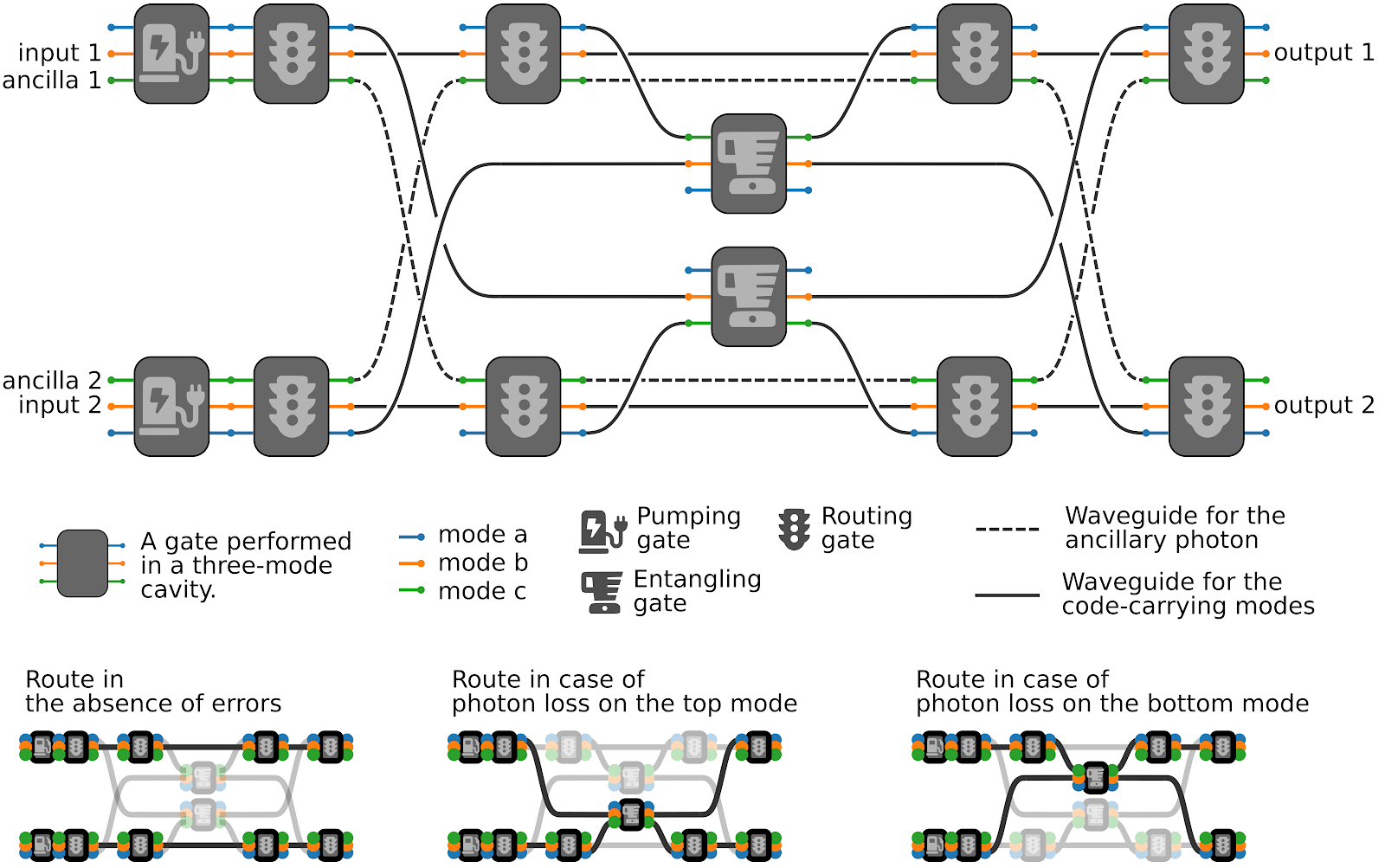
Similar design work
Similar design work

- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics
Similar design work


- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks
Similar design work



- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
- Krastanov et al.Controlled-Phase Gate by Dynamic Coupling of Photons to a Two-Level Emitter
- Basani et al. (me as last author)All-Photonic Artificial Neural Network Processor Via Non-linear Optics
- Krastanov et al.Universal control of an oscillator with dispersive coupling to a qubit
- Krastanov et al.Optically-Heralded Entanglement of Superconducting Systems in Quantum Networks
- Raniwala*, Krastanov* et al.A spin-optomechanical quantum interface [...]
Digital Quantum Hardware
Optimized Entanglement Purification




- Krastanov et al.Art installation on Non-contextual Hidden Variable theories
They can be noisy!
Desired:
\[\begin{aligned} A=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ \end{aligned}\]The hardware generated:
90% chance for \[\begin{aligned} A=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ \end{aligned}\] 10% chance for a bit flip on Bob's qubit \[\begin{aligned} C=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ \end{aligned}\]Purification of entanglement
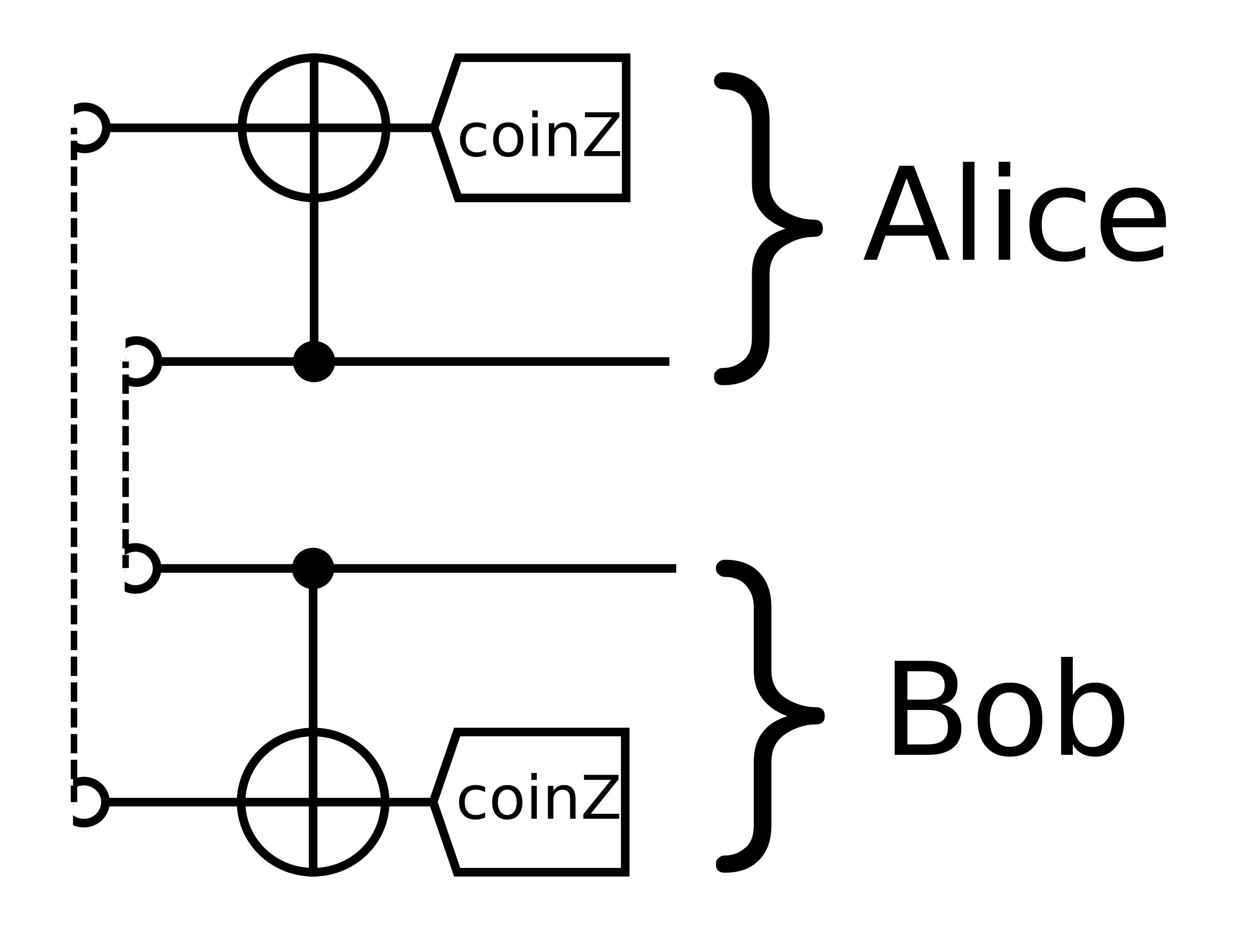

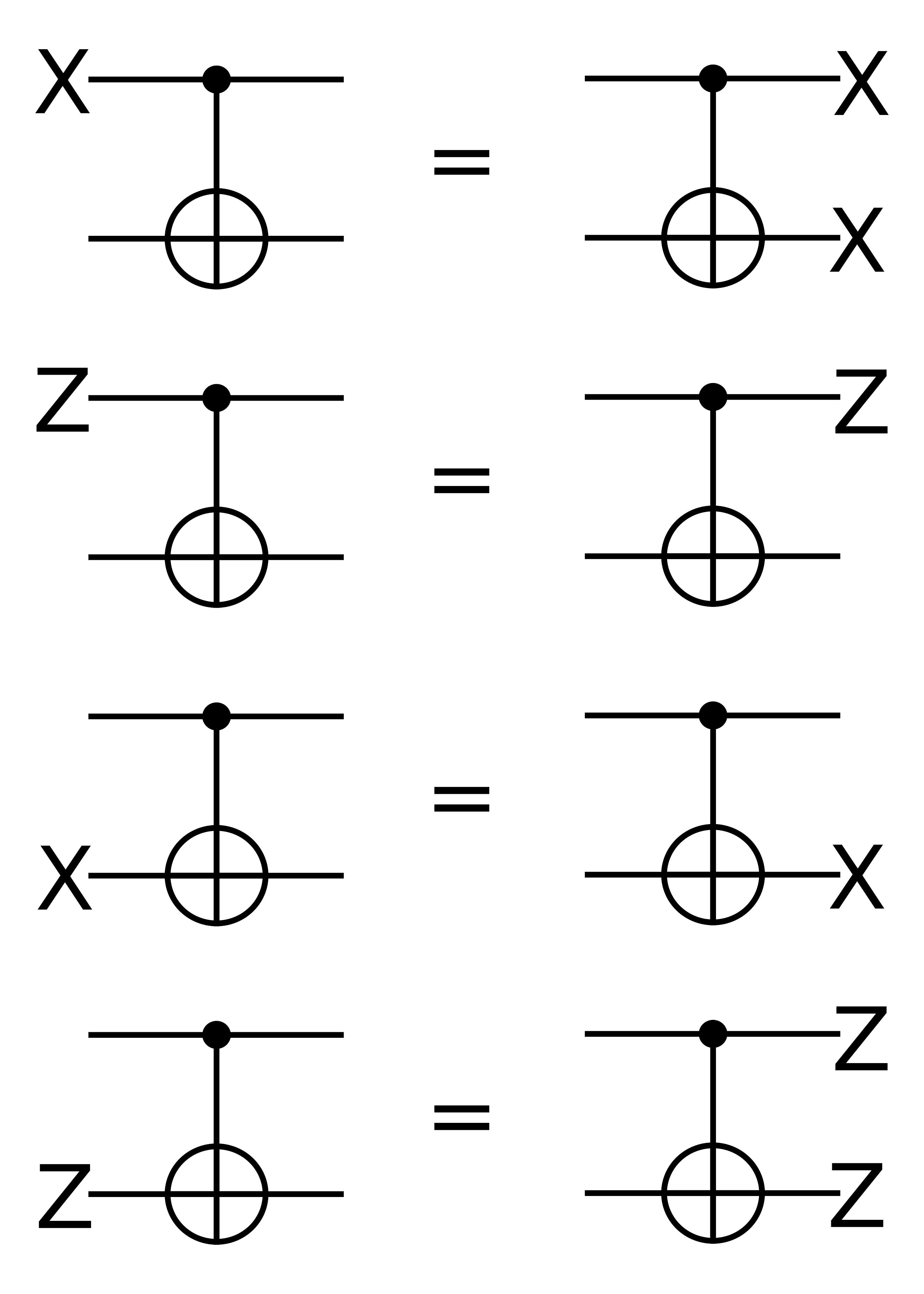

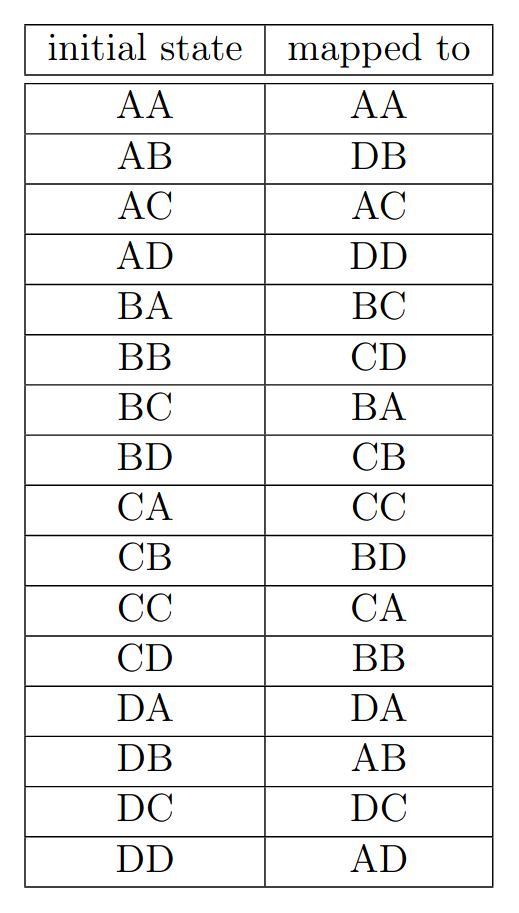


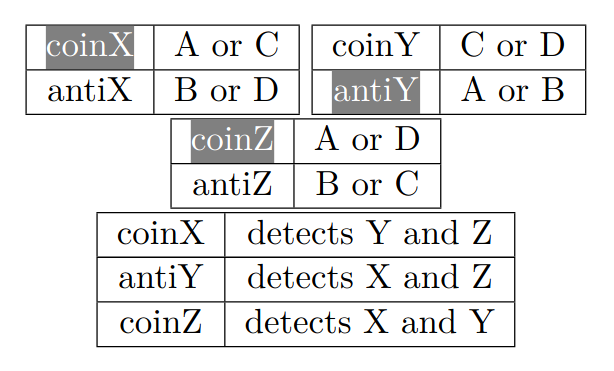
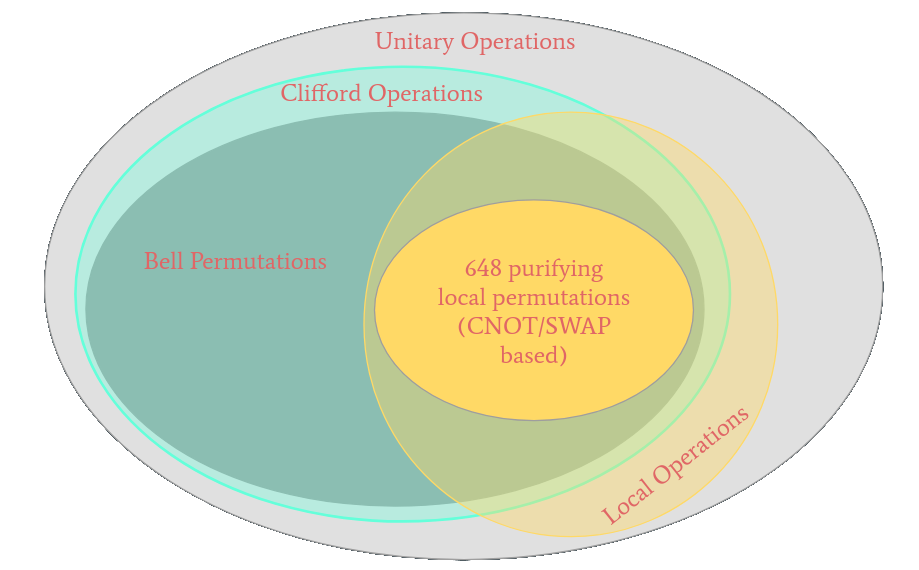
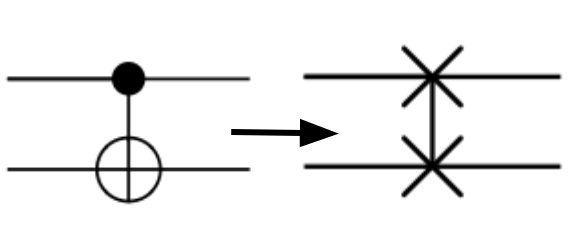
What if we want multi-sacrifice circuit?
Discrete Optimization: Evolutionary Algorithm
Discrete Optimization: Evolutionary Algorithm
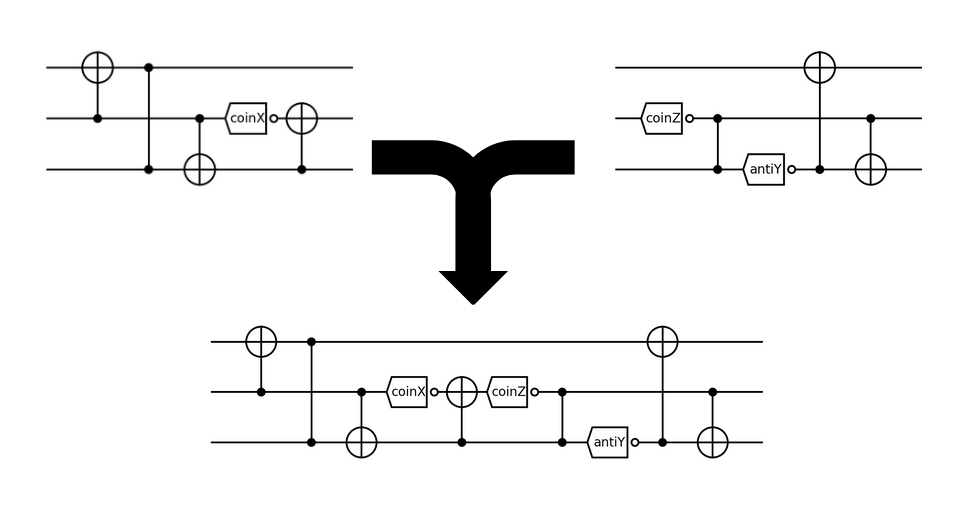
Discrete Optimization: Evolutionary Algorithm

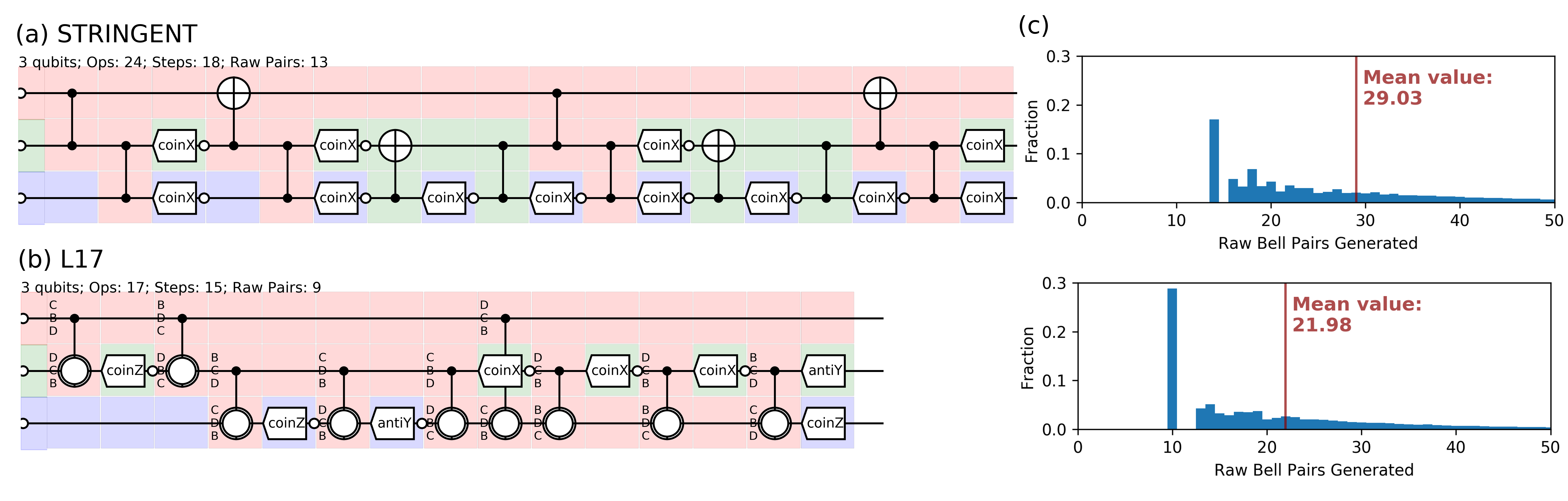
(c) resource usage for each
- Krastanov et al.Optimized Entanglement Purification
- Krastanov et al.Optimized Entanglement Purification

- Krastanov et al.Optimized Entanglement Purification
Continuing and Future Projects
Continuing and Future Projects
Purification of more general resource states¹²
Clifford simulators orders of magnitude better than alternatives²
Rigorous theory bounds on purification performance³
- Krastanov et al.Heterogeneous Multipartite Entanglement Purification for Size-Constrained Quantum Devices
- me and undergrads under my advisementQuantumClifford.jl software package
- recently started conversation with colleagues at Delft
Full-Stack Design and Optimization Toolkit
Types of Dynamics
Types of Dynamics

Hamiltonians, Master Equations
Types of Dynamics

Hamiltonians, Master Equations
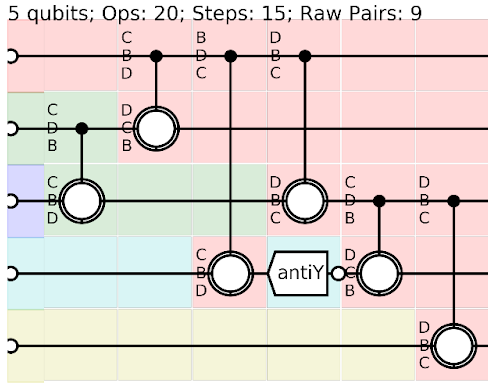
Gates, Circuits
Types of Dynamics

Hamiltonians, Master Equations

Gates, Circuits
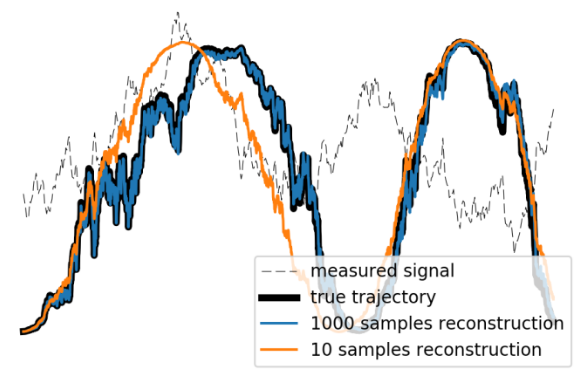
Weak Measurements, Feedback
State Representation

Continuous evolution at one layer, followed by noisy Clifford circuit simulator...
... and discrete event simulators
... and support for symbolic algebra systems
... running on computational accelerators like GPUs
... support for other formalisms
... all of this, with auto-differentiation and reverse design
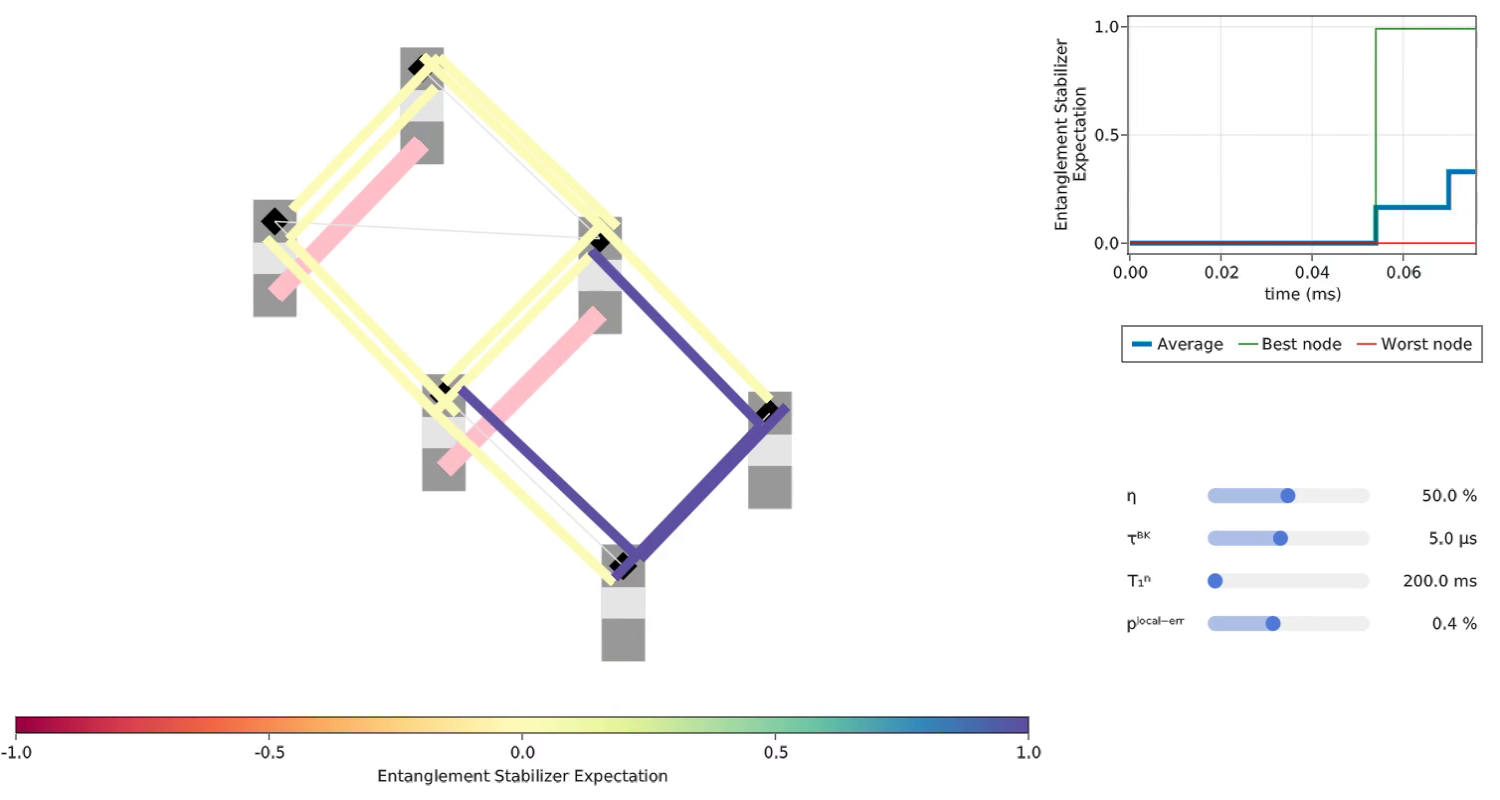
- Dong et al.High-speed programmable photonic circuits in a cryogenically compatible, visible–near-infrared 200 mm CMOS architecture

- Dong et al.High-speed programmable photonic circuits in a cryogenically compatible, visible–near-infrared 200 mm CMOS architecture
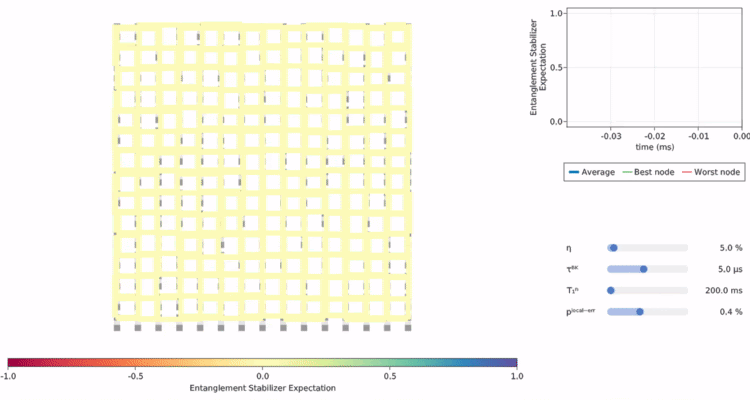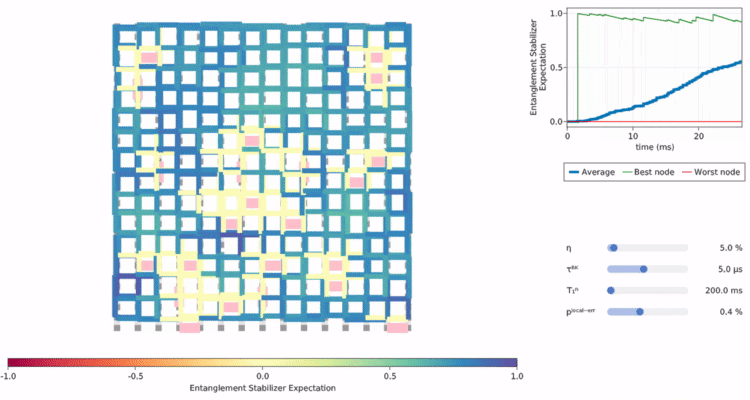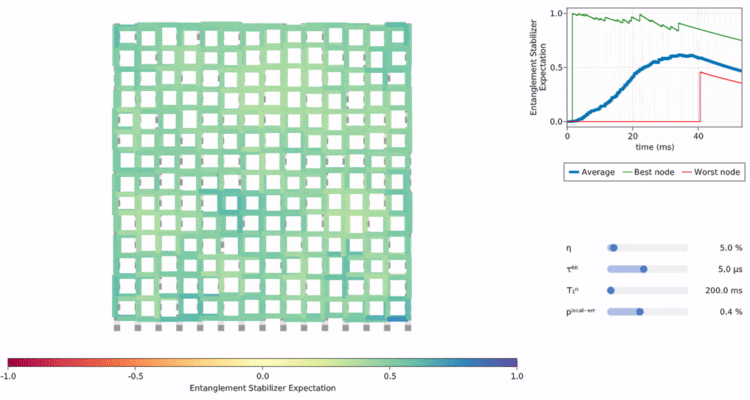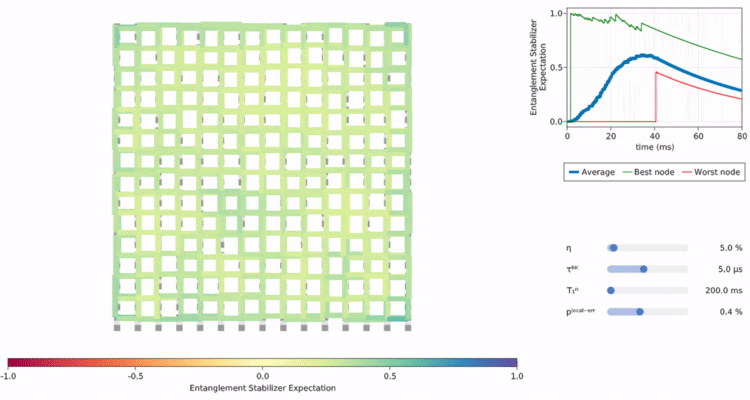
low-level hardware control,
resource purification,
optimization of error-correcting codes,
quantum network protocols,
and generally co-design across the layers of the technology stack.