Faster-than-Clifford Simulations of Entanglement Purification Circuits
and Their Full-stack Optimization

Vaishnavi L. Addala¹, Shu Ge¹, Stefan Krastanov^1,2

¹Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA
²College of Information and Computer Sciences, University of Massachusetts Amherst, 140 Governors Drive Amherst, Massachusetts 01003, USA

We develop a faster algorithm for simulating entanglement purification by representing purification gates as permutations.
This allows us to run otherwise intractable optimizations, generating purification circuits better than state of the art.

How to represent n Bell pairs and how much it costs

\[ \underbrace{A\otimes B\dots}_{n\text{ pairs}} \]

\[ \left.\begin{pmatrix}0\\1\\0\\\vdots\\0\end{pmatrix}\right\}\scriptsize \mathcal{O}(2^{2n}) \]

State Vector

\[ \left.\begin{bmatrix}+&XX&\\+&ZZ&\\&&\ddots\end{bmatrix}\right\}\scriptsize \mathcal{O}(n\times n) \]

Stabilizer Tableau

\[ \underbrace{0011\dots}_{2n \text{ bits}} \]

Our Approach

It is exponentially prohibitive to represent the state of a large entanglement purification circuit as state vectors. The Clifford formalism provides a viable alternative. We provide an even faster alternative, with a new state representation datastructure.

Our $\mathcal{O}(n)$ representation

\[A\otimes B\otimes D \sim\begin{bmatrix}+&XX&II&II\\+&ZZ&II&II\\ -&II&XX&II\\-&II&ZZ&II\\ +&II&II&XX\\-&II&II&ZZ\end{bmatrix} \sim \begin{bmatrix}+&XX&&\\+&ZZ&&\\ -&&XX&\\-&&ZZ&\\ +&&&XX\\-&&&ZZ\end{bmatrix} \sim \begin{pmatrix}+\\+\\-\\-\\+\\-\end{pmatrix}\]

\[\sim 0, 0, 1, 1, 0, 1\]

Bell state tableaux are block-diagonal and purification circuits only permute the Bell basis. Only the column of phases changes as the circuit evolves. Thus, we can represent the state of a circuit as a bitstring of length $2n$ where $n$ is the number of Bell pairs (one bit per phase).

Our $\mathcal{O}(1)$ purification gate

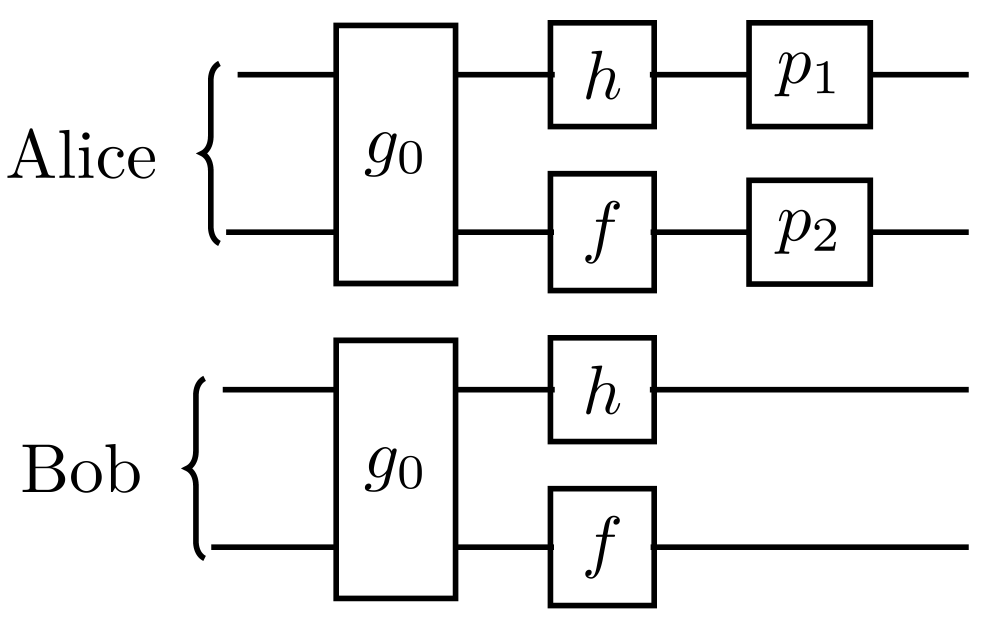
$ p_1,\ p_2 \in \mathcal{P}_1 $ (Paulis)

$ h,\ f \in\mathcal{C}^*_1 $ (no-phase Cliffords)

$ g_0 \in Q = \mathcal{C}^*_2 / (\mathcal{C}^*_1\otimes\mathcal{C}^*_1) $
(inherently two-qubit Cliffords)

This is the most general form of a Bell purification gate (a permutation of the Bell basis).
Its simulation takes us nanoseconds.
The number of such gates is
$|\mathcal{P}_1|^2\times|\mathcal{C}_1^*|^2\times|Q|=4^2\times6^2\times20=11520$

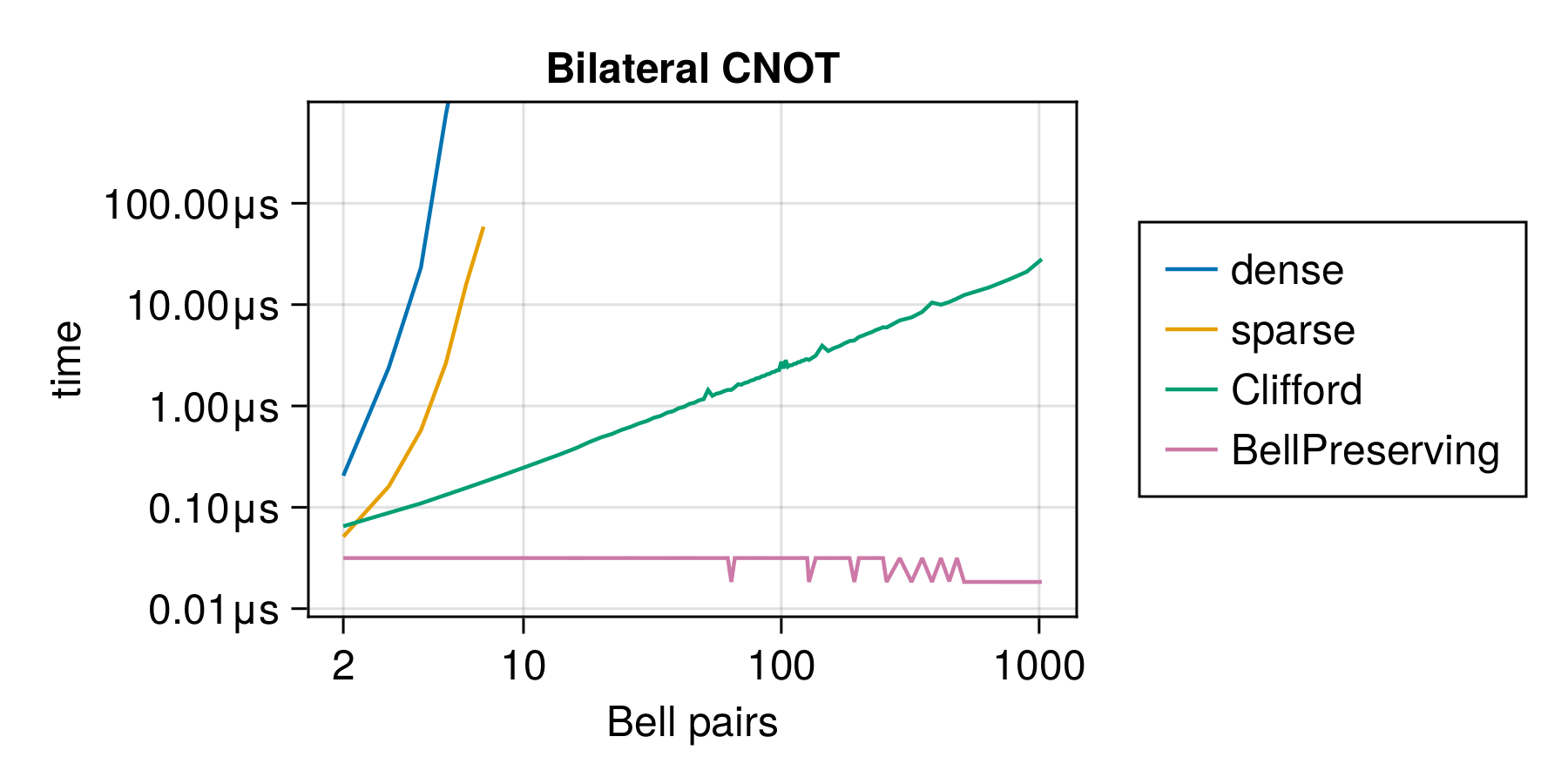
Benchmarks

Benchmarking our "Bell Preserving" simulator against state-of-the-art dense and sparse state vector simulators and Clifford simulators. Plotted is time to perform a bilateral CNOT vs the size of the system, for a number of different formalisms.

The "Good gates" subgroup

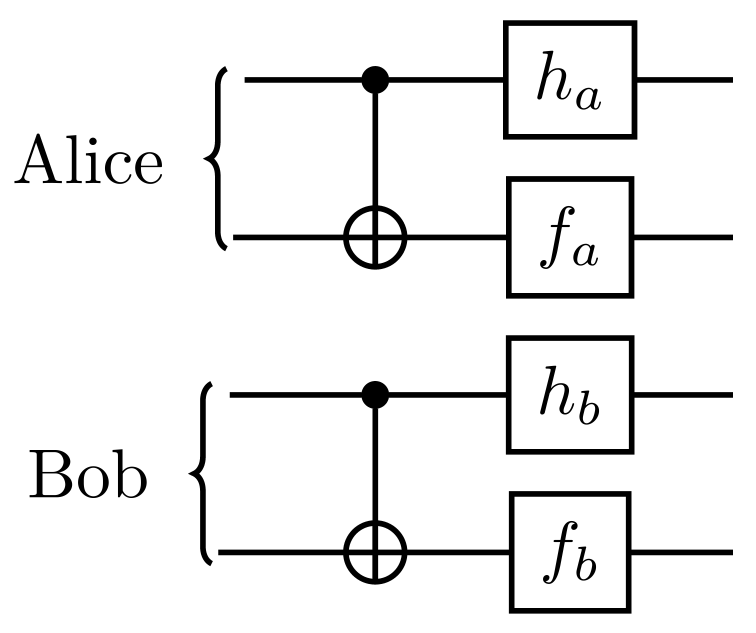
$ h_a\otimes f_a,\ h_b\otimes f_b \in S_3 $

one of the six permutations
of the {B,C,D} set

In practice we might prefer to use only the "good" subset of Bell permutations, namely the $6\times6$ gates of the form above which always map $A\otimes A \mapsto A\otimes A$.

Application: Full-stack Codesign,
i.e. Your Usual Choice of "Fidelity" is Bad

A riddle about a typical networking protocol:

Start with $N$ noisy Bell pairs.
Purify them down to $n$ pairs.
Use an [n,k,d] code to teleport $k$ logical qubits.

You can use our fast optimizer to make a purification circuit. What are you supposed to maximize?

If you said "entanglement fidelity" you would be wrong. Can you see why?

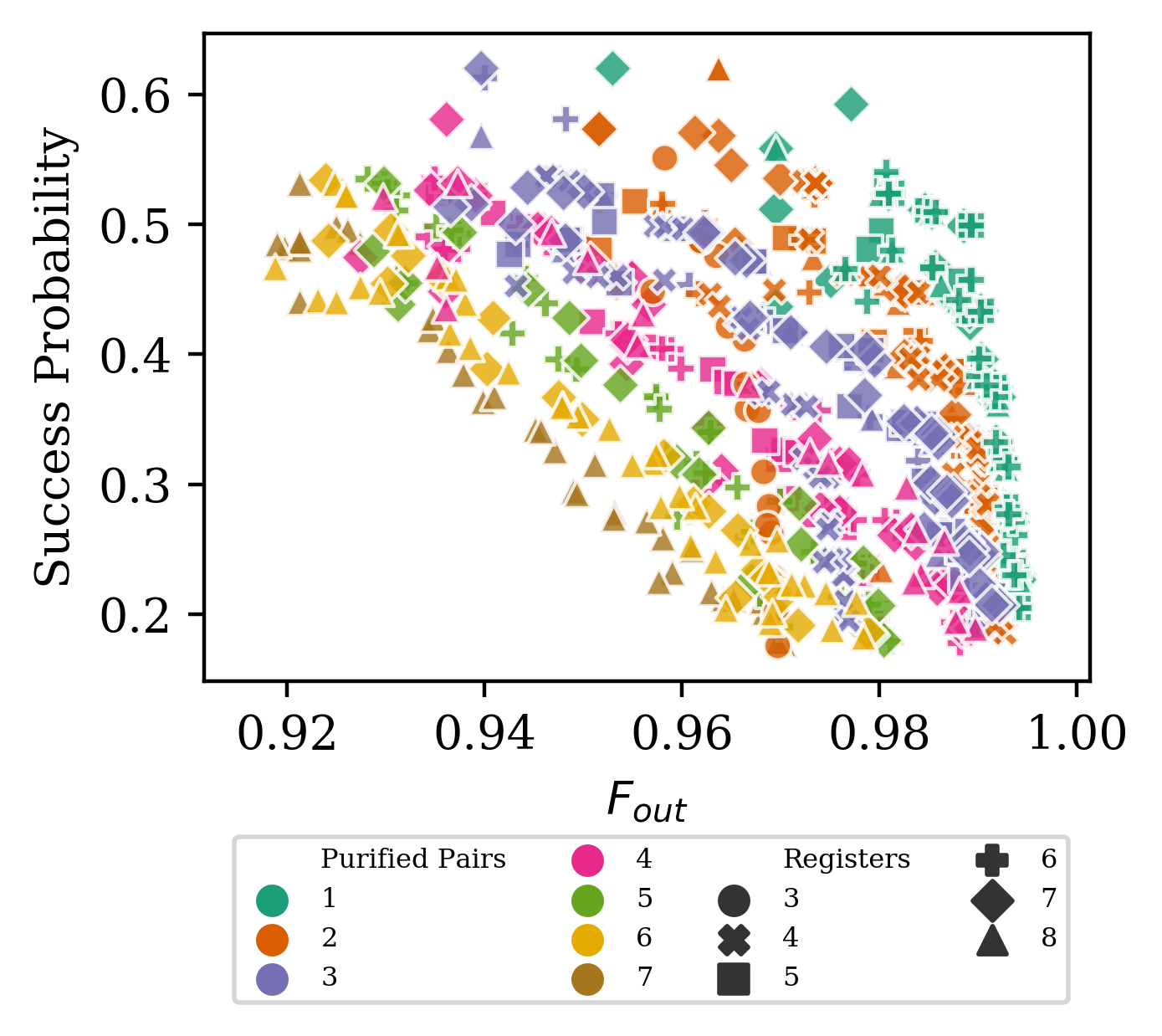
To help, we plot the probability to succeed at teleporting vs the fidelity of raw pairs, for three different optimization targets.

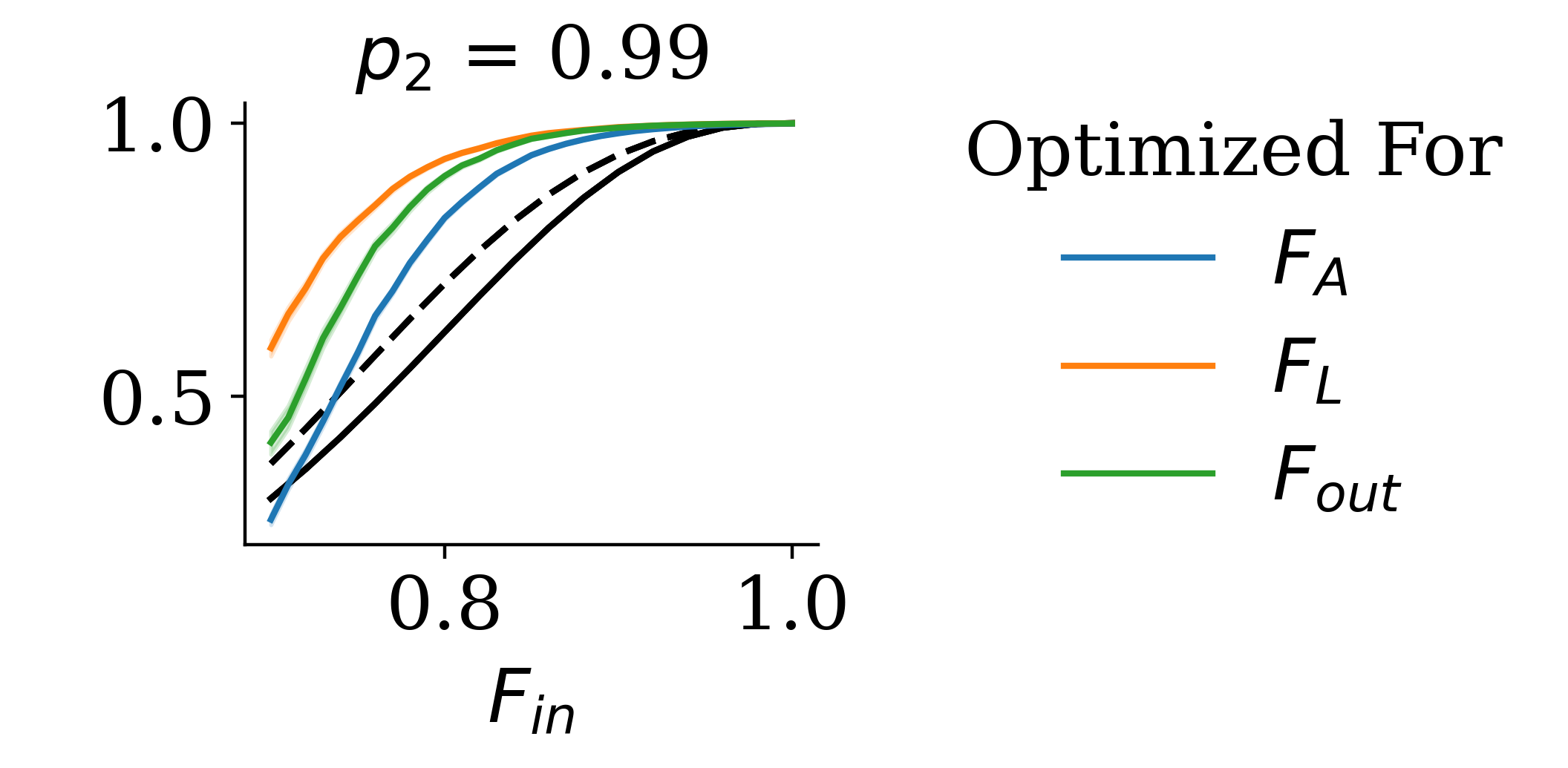
$F_A$ is typical multipair fidelity $F_{out}$ is average single-pair fidelity
$F_L$ is probability for less than $\frac{d}{2}$ errors after purification

Application: Generating a whole zoo of circuits optimized for particular hardware constraints

Each dot represents the performance of a circuit.

Notation (and some background)

\[\begin{aligned} A\propto|00\rangle+|11\rangle\\ B\propto|01\rangle-|10\rangle\\ C\propto|01\rangle+|10\rangle\\ D\propto|00\rangle-|11\rangle \end{aligned}\]

Bell State Basis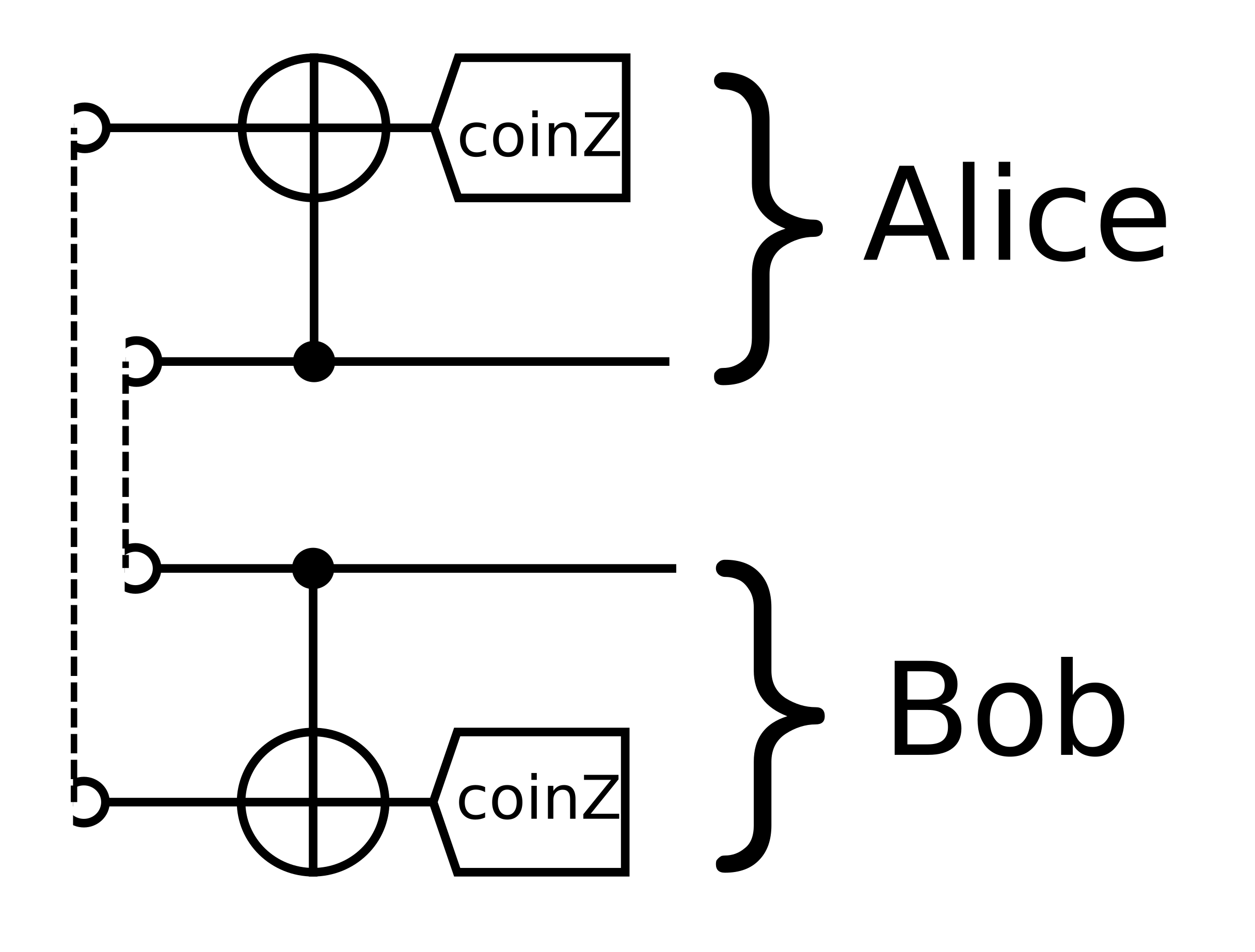

Purification Circuit

Conclusions and Outlook

We provide a drastically faster simulation algorithm for entanglement circuits: $\mathcal{O}(1)$ instead of $\mathcal{O}(n)$

We provide optimizers that employ the faster simulator to generate purification circuits, bespokely optimized for size- and noise-constrained hardware, better than anything else in the literature.

Through full-stack optimizations, we show that the typical figures of merit in the literature are poor choices when optimizing a complete system.

Link to our work: Addala, Ge, Krastanov, "Faster-than-Clifford Simulations of Entanglement Purification Circuits and Their Full-stack Optimization", (arXiv:2307.06354)

Faster-than-Clifford Simulations of Entanglement Purification Circuitsand Their Full-stack Optimization

Vaishnavi L. Addala1, Shu Ge1, Stefan Krastanov1,2

1Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA 2College of Information and Computer Sciences, University of Massachusetts Amherst, 140 Governors Drive Amherst, Massachusetts 01003, USA

We develop a faster algorithm for simulating entanglement purification by representing purification gates as permutations. This allows us to run otherwise intractable optimizations, generating purification circuits better than state of the art.