From Better Entanglement Distillation to Multi-formalism Quantum Simulation Tools for the Entire Network Stack

Stefan Krastanov
MIT ⟶ UMass Amherst

The Quantum Technology Stack

Materials

Analog Control

Noisy Digital Circuits

Error Correction

Quantum Algorithms

Optimizing Entanglement Distilation

Alice has a qubit
Alice has a qubit
Bob too
They can be entangled! \[\begin{aligned} A=|\phi_{+}\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ B=|\psi_{-}\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}}\\ C=|\psi_{+}\rangle=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ D=|\phi_{-}\rangle=\frac{|00\rangle-|11\rangle}{\sqrt{2}} \end{aligned}\]
They can be entangled! \[\begin{aligned} A=|\phi_{+}\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ B=|\psi_{-}\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}}\\ C=|\psi_{+}\rangle=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ D=|\phi_{-}\rangle=\frac{|00\rangle-|11\rangle}{\sqrt{2}} \end{aligned}\]
Hidden Variable theories¹
  1. Krastanov et al.
    Art installation on Non-contextual Hidden Variable theories

They can be noisy!

Desired:

\[\begin{aligned} A=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ \end{aligned}\]

The hardware generated:

90% chance for \[\begin{aligned} A=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ \end{aligned}\] 10% chance for a bit flip on Bob's qubit \[\begin{aligned} C=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ \end{aligned}\]

Purification of entanglement

\[\begin{aligned} A=|\phi_{+}\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\\ B=|\psi_{-}\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}}\\ C=|\psi_{+}\rangle=\frac{|01\rangle+|10\rangle}{\sqrt{2}}\\ D=|\phi_{-}\rangle=\frac{|00\rangle-|11\rangle}{\sqrt{2}} \end{aligned}\]
Simple entanglement purification circuit
\[\begin{aligned} A\propto|00\rangle+|11\rangle\\ B\propto|01\rangle-|10\rangle\\ C\propto|01\rangle+|10\rangle\\ D\propto|00\rangle-|11\rangle \end{aligned}\]
Purification as error propagation and detection
\[\begin{aligned} A\propto|00\rangle+|11\rangle\\ B\propto|01\rangle-|10\rangle\\ C\propto|01\rangle+|10\rangle\\ D\propto|00\rangle-|11\rangle \end{aligned}\]
Purification as reshuffling of probabilities
\[\begin{aligned} A\propto|00\rangle+|11\rangle\\ B\propto|01\rangle-|10\rangle\\ C\propto|01\rangle+|10\rangle\\ D\propto|00\rangle-|11\rangle \end{aligned}\]
Purification as reshuffling of probabilities
Possible coincidence measurements

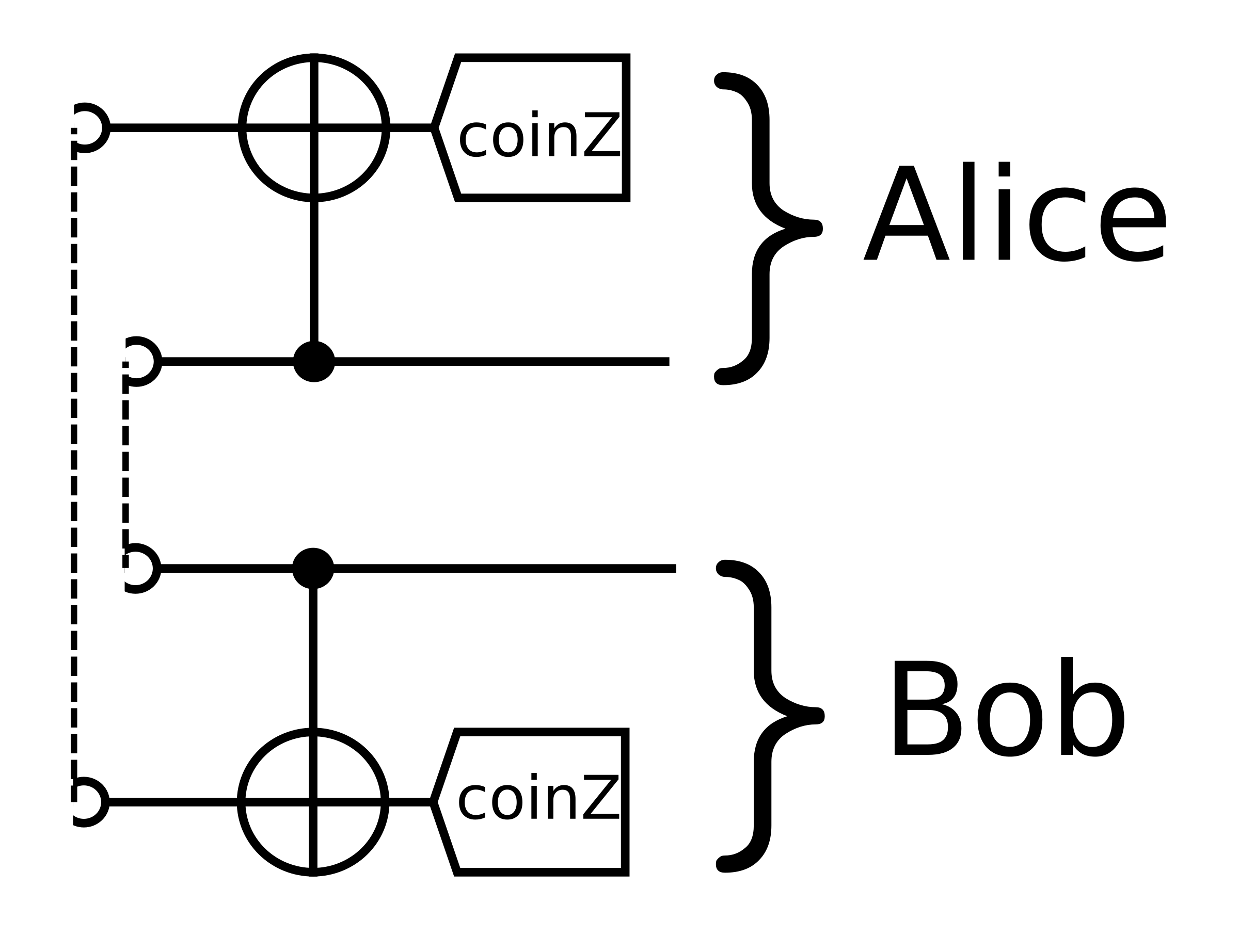
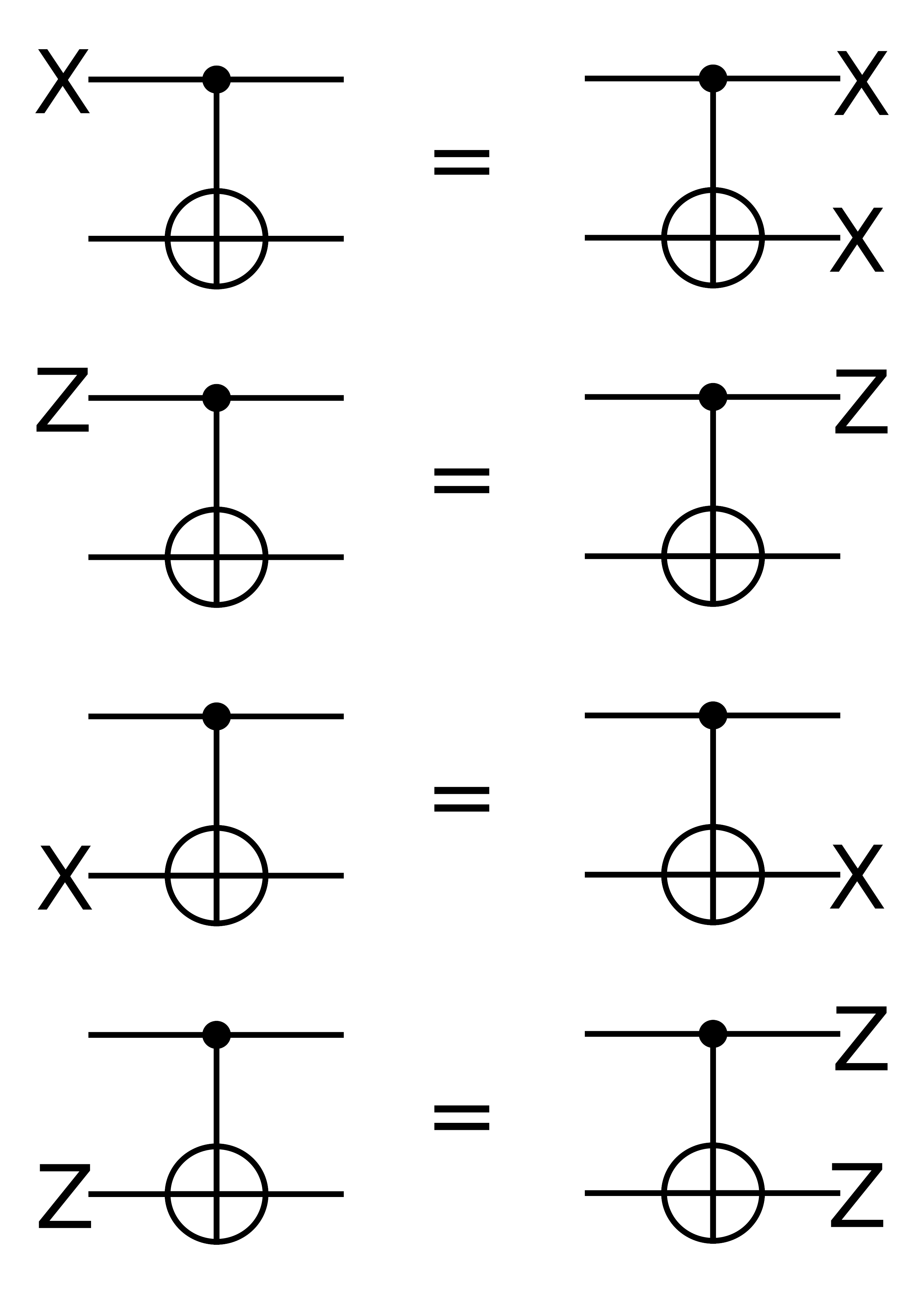
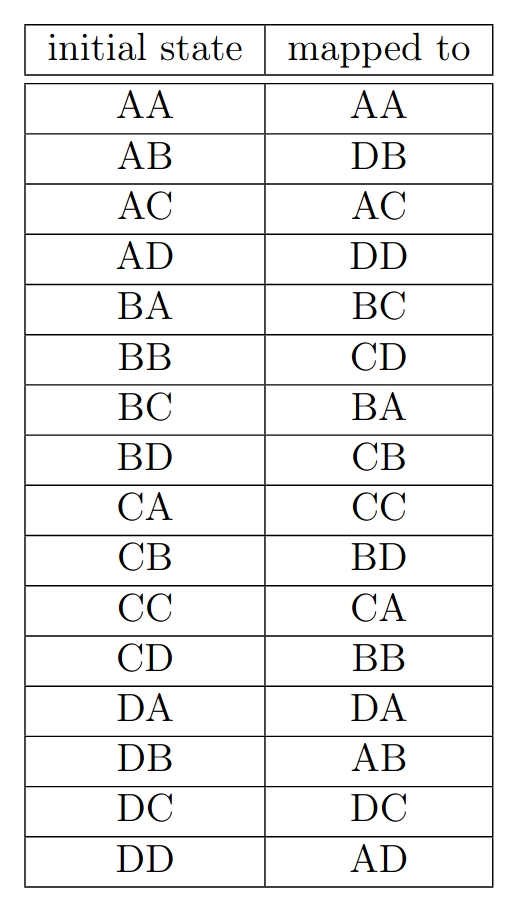
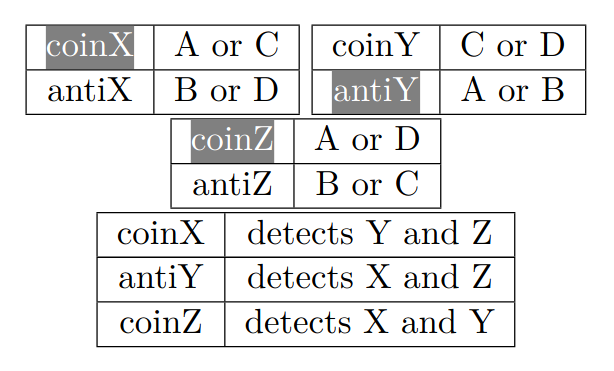
A convenient representation for the density matrix

A hypercube of probabilities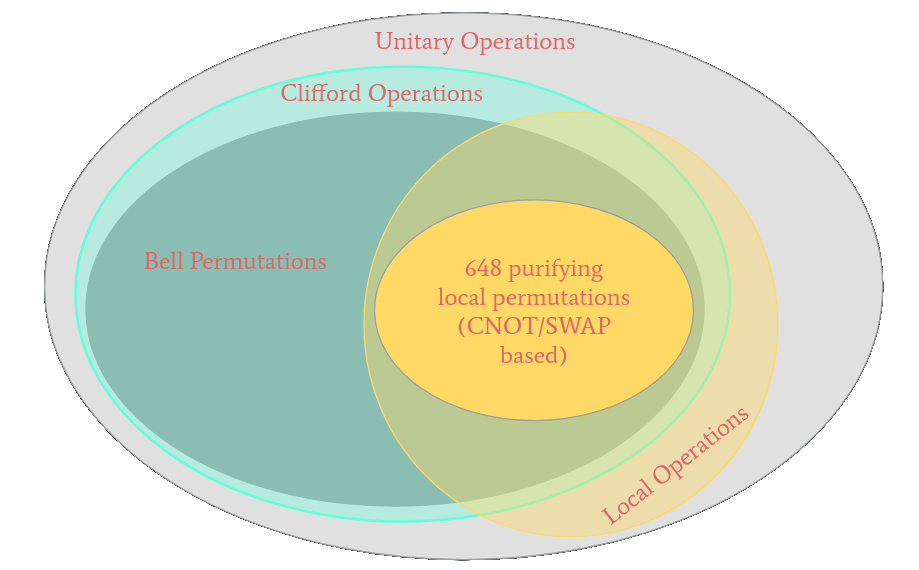
\[\begin{aligned} A\propto|00\rangle+|11\rangle\\ B\propto|01\rangle-|10\rangle\\ C\propto|01\rangle+|10\rangle\\ D\propto|00\rangle-|11\rangle \end{aligned}\]
... How are we going to find the "good" permutation?
What if we want multi-sacrifice circuit?

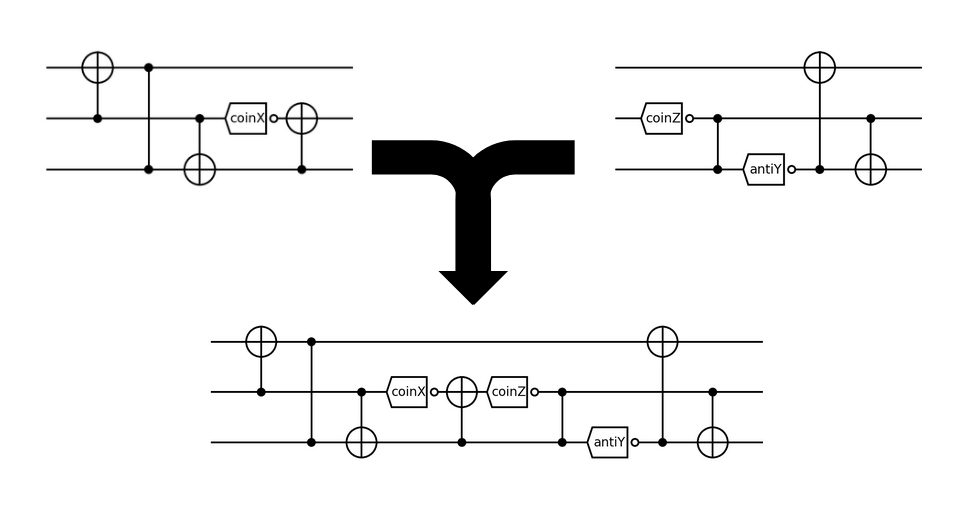
Discrete Optimization: Evolutionary Algorithm

Discrete Optimization: Evolutionary Algorithm

Mutations

Discrete Optimization: Evolutionary Algorithm

Mutations
Offspring circuits
Optimized circuits for purification¹, better than any known circuits.
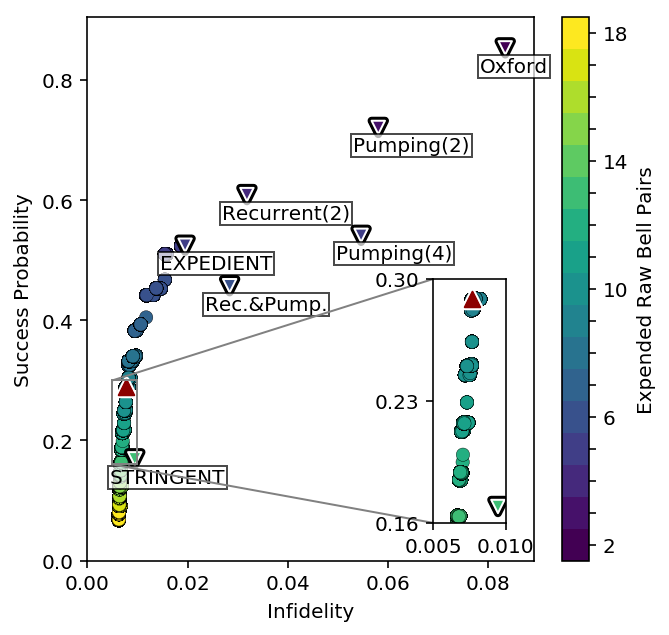
  1. Krastanov et al.
    Optimized Entanglement Purification
  2. Jansen et al.
    Enumerating all bilocal Clifford distillation protocols through symmetry reduction

n-to-k purification protocols¹

  1. Vaishnavi Addala, Stefan Krastanov
Purification protocols with varying sacrificial pairs, purified pairs, and register width.
A minimum-width register is necessary. Here, with n-to-2 purification examples, we need a width of 4.
A typical 5-to-2 purification circuit on a small register.
What figure of merit should we be using?
The hypercube of probabilities describing the state of 3 noisy Bell pairs.

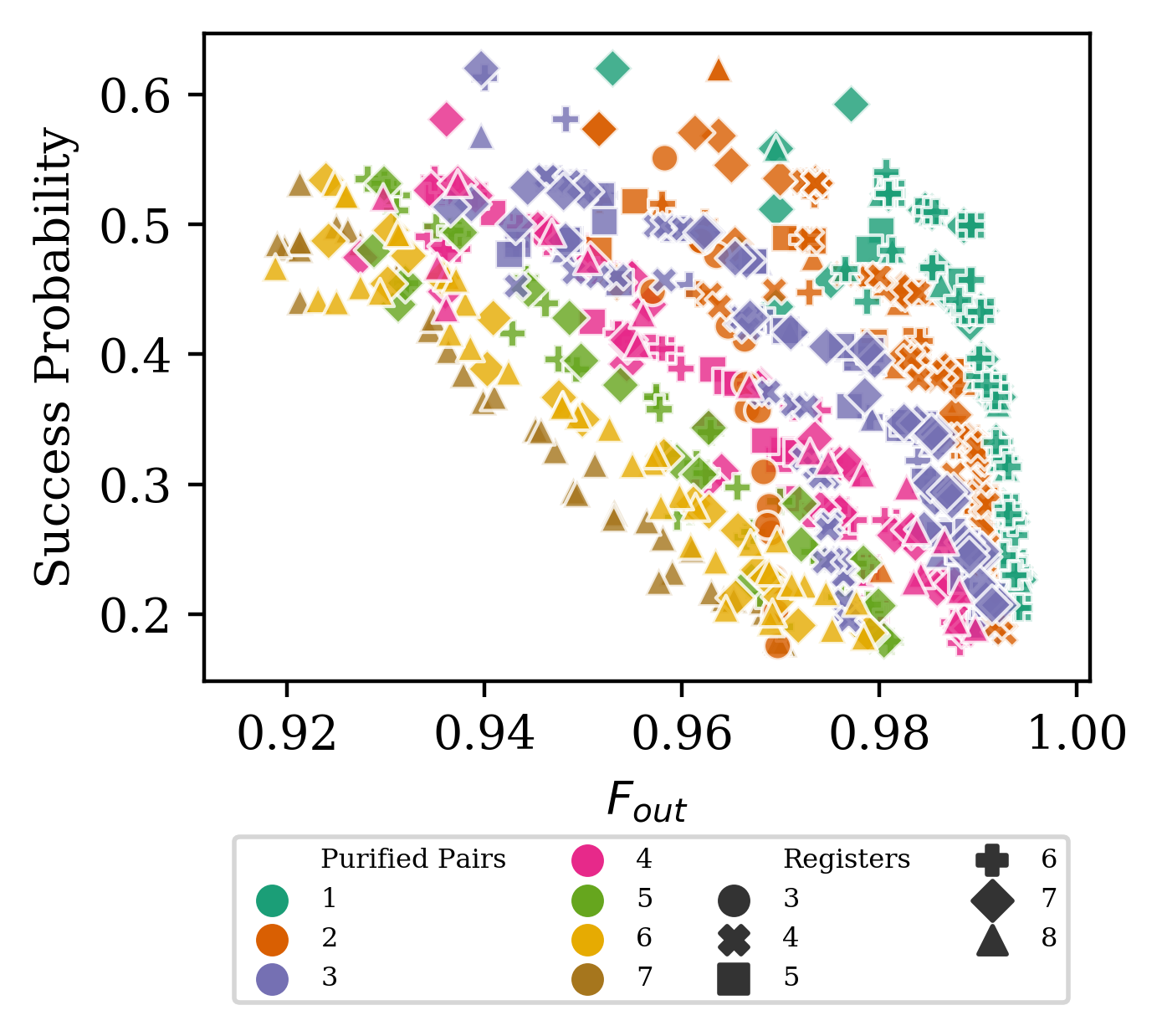
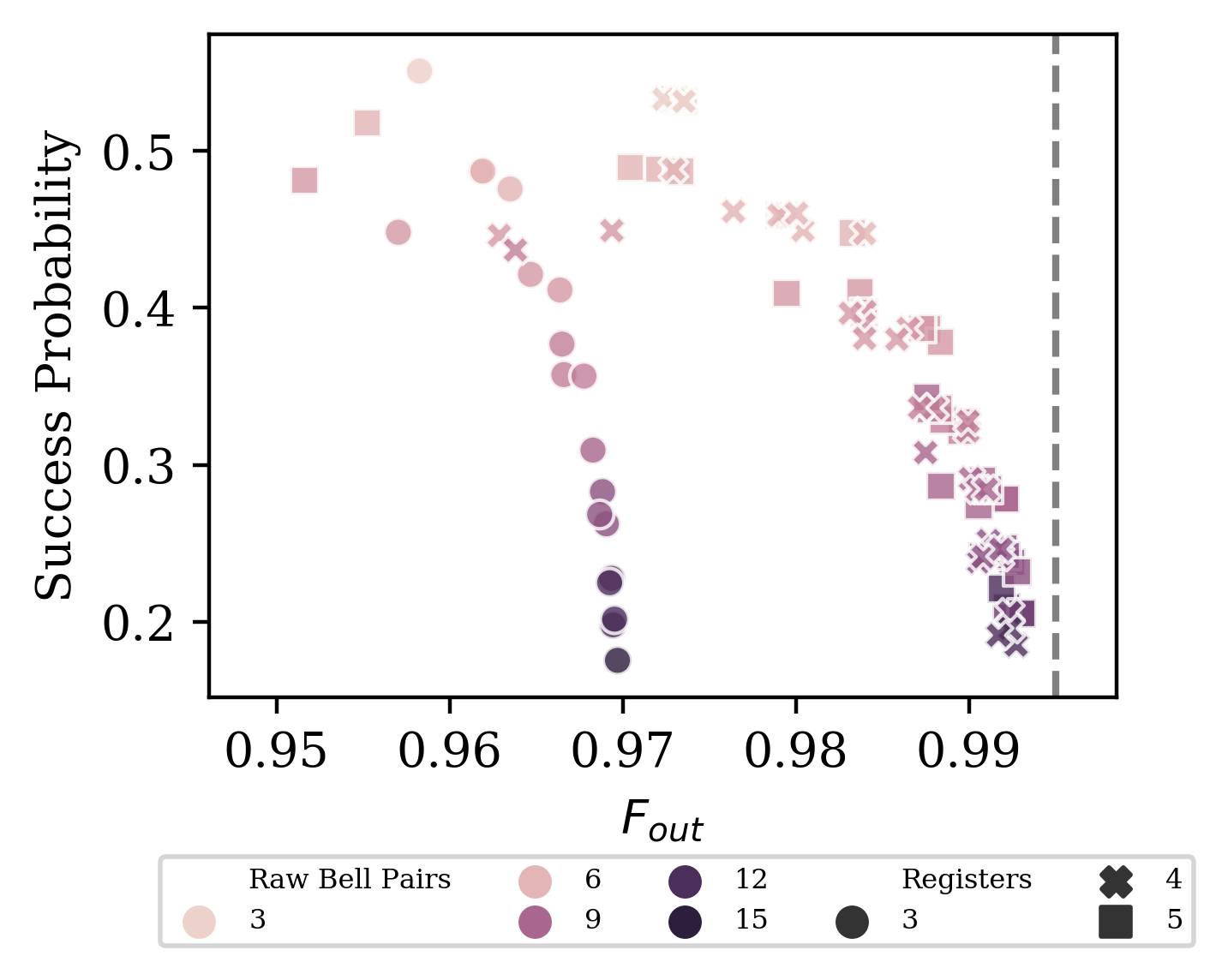
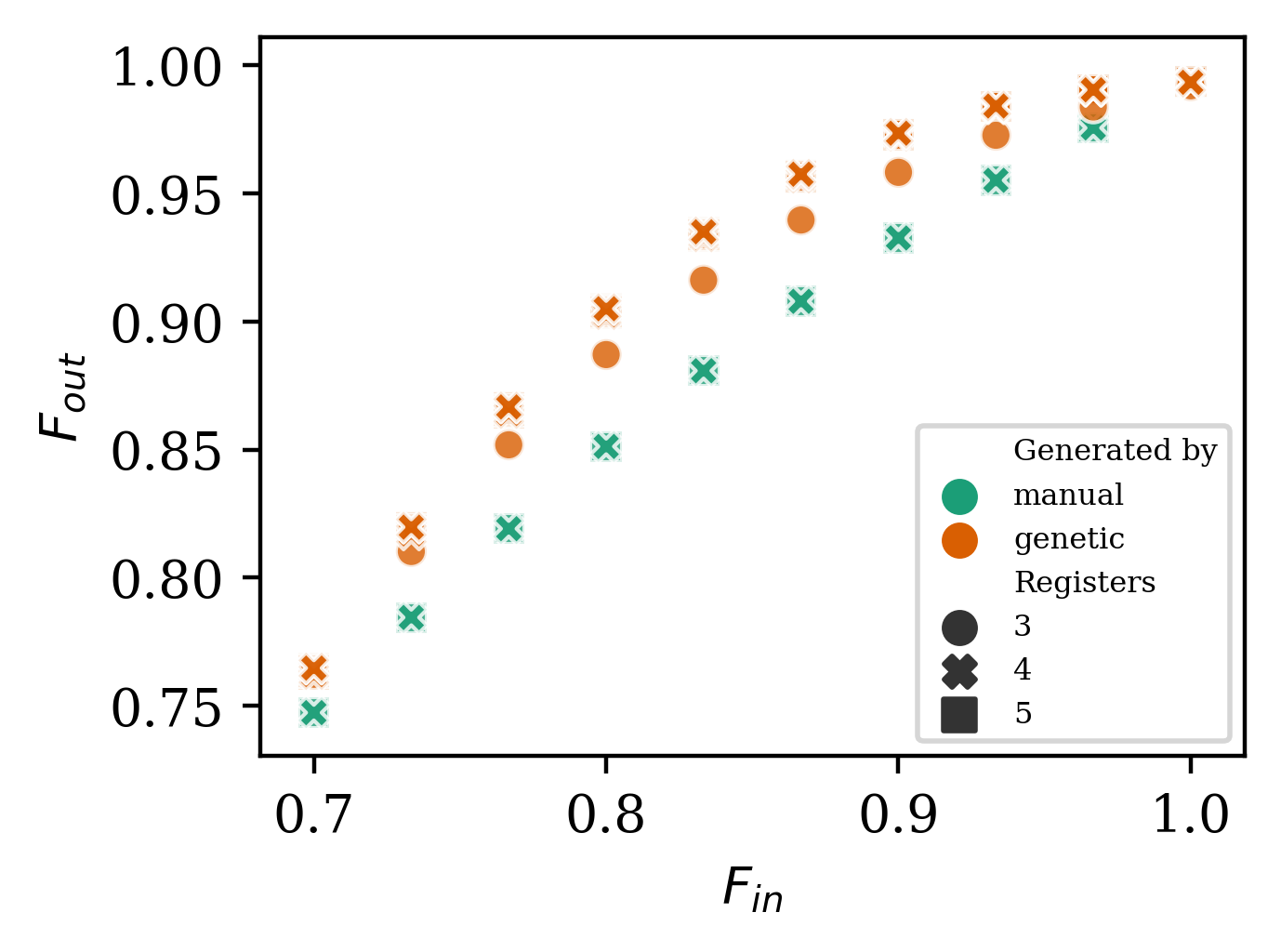
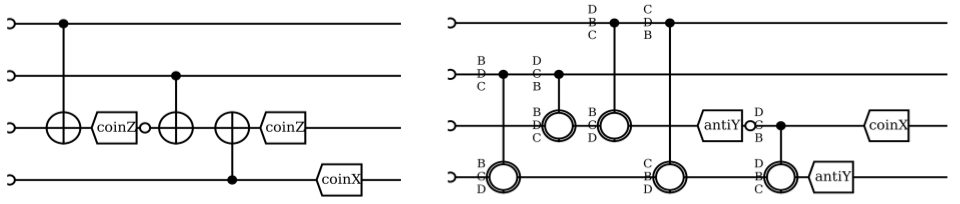
Optimizatin of concatenated
purification ⟶ ECC teleportation
protocols¹

  1. Vaishnavi Addala, Stefan Krastanov
For teleportation without ECC.
For distance 3 codes (1 correctable error)
For distance 5 codes (2 correctable errors)
14-to-11 purification followed by a teleportation of a [[11,2,5]] code. Each line is a differently optimized circuit.

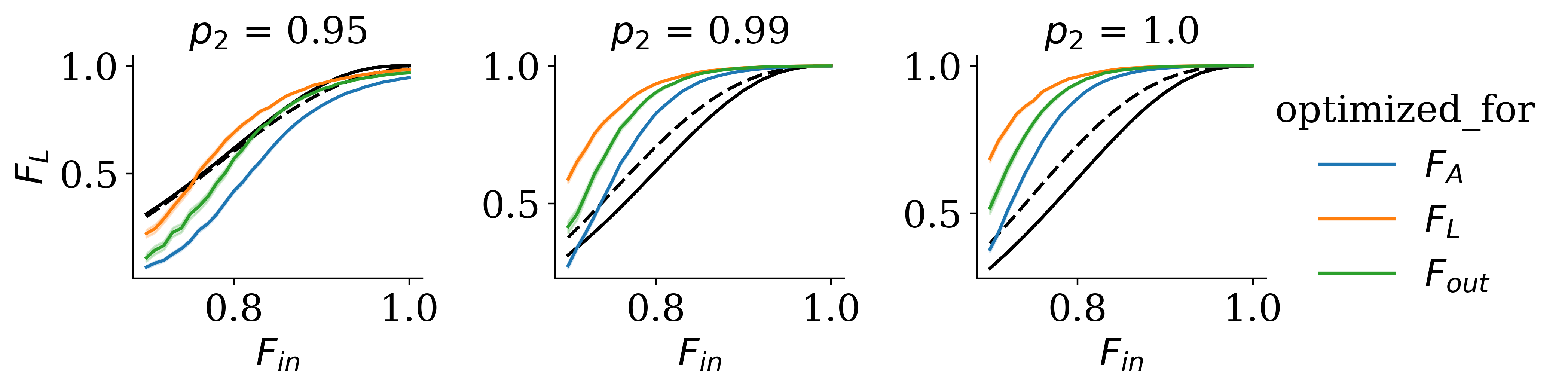
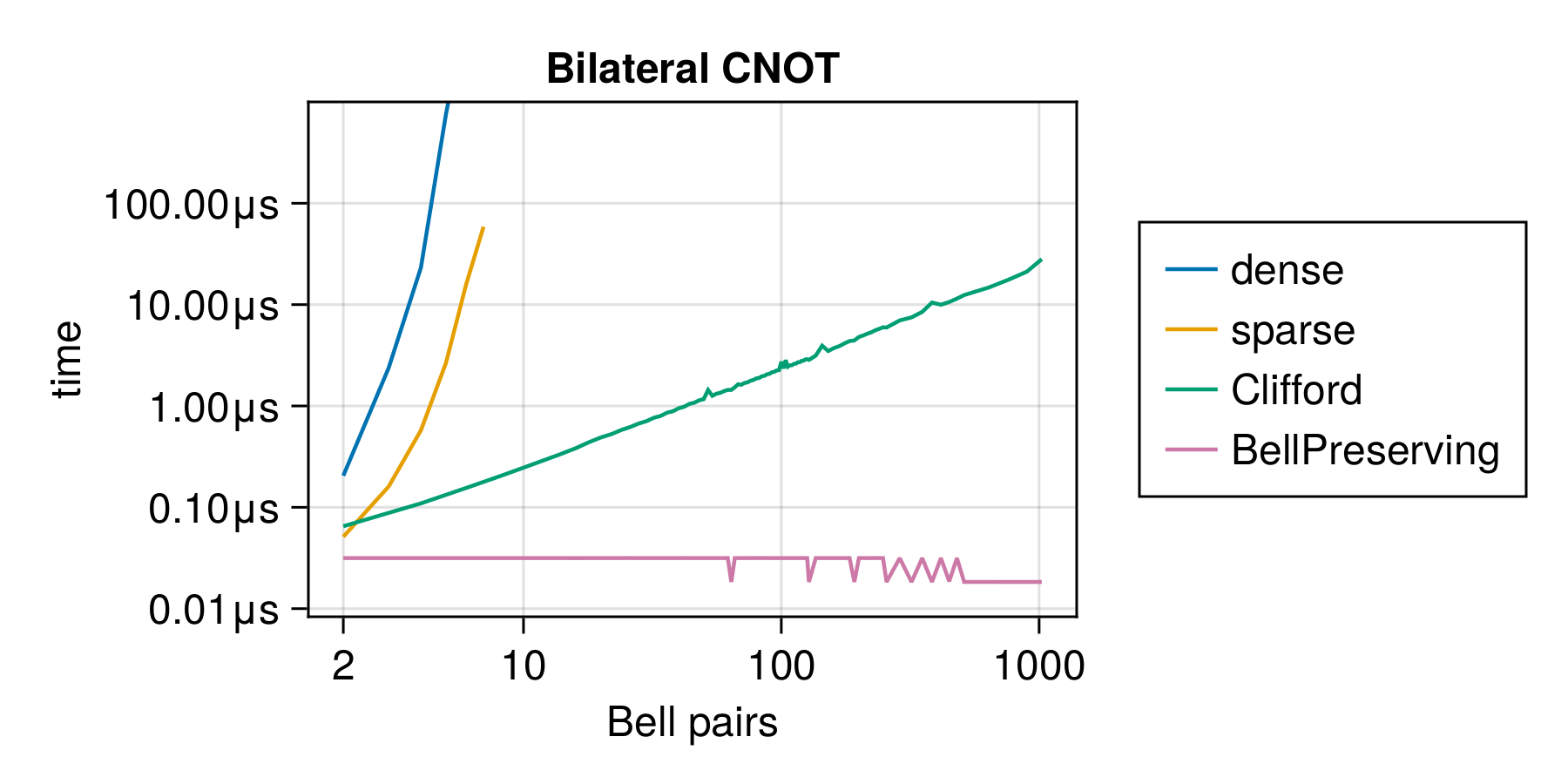
Modeling Entanglement More Efficiently¹

  1. Shu Ge, Stefan Krastanov

Error-detection circuits are Clifford circuits

Clifford circuits are efficient to simulate on stabilizer states
\[\begin{aligned} A\propto|00\rangle+|11\rangle \sim\begin{bmatrix}+&XX\\+&ZZ\end{bmatrix}\\ B\propto|01\rangle-|10\rangle \sim\begin{bmatrix}-&XX\\-&ZZ\end{bmatrix}\\ C\propto|01\rangle+|10\rangle \sim\begin{bmatrix}-&XX\\+&ZZ\end{bmatrix}\\ D\propto|00\rangle-|11\rangle \sim\begin{bmatrix}+&XX\\-&ZZ\end{bmatrix} \end{aligned}\]
\[A\otimes B\otimes D \sim\begin{bmatrix}+&XX&II&II\\+&ZZ&II&II\\ -&II&XX&II\\-&II&ZZ&II\\ +&II&II&XX\\-&II&II&ZZ\end{bmatrix}\]
\[A\otimes B\otimes D \sim\begin{bmatrix}+&XX&&\\+&ZZ&&\\ -&&XX&\\-&&ZZ&\\ +&&&XX\\-&&&ZZ\end{bmatrix}\]
Bell state tableaux are block-diagonal and error-detection circuits only permute the Bell basis!
\[A\otimes B\otimes D \sim\begin{matrix}+&\phantom{XX}&\phantom{XX}&\phantom{XX}\\+&&&\\ -&&&\\-&&&\\ +&&&\\-&&&\end{matrix}\]
Bell state tableaux are block-diagonal and error-detection circuits only permute the Bell basis!

\[ \underbrace{A\otimes B\dots}_{n\text{ pairs}} \]

\[ \left.\begin{pmatrix}0\\1\\0\\\vdots\\0\end{pmatrix}\right\}\scriptsize \mathcal{O}(2^n) \]

\[ \left.\begin{bmatrix}+&XX&\\+&ZZ&\\&&\ddots\end{bmatrix}\right\}\scriptsize \mathcal{O}(n\times n) \]

\[ \underbrace{0011\dots}_{2n \text{ bits}} \]

What (bi-local) gates exist in this more efficient formalism?
  • Let us call them "Bell Permuting" or "Bell Preserving" gates
  • Let us denote them $\mathrm{BP}(n)$
  • Permuting gates are Clifford gates
  • Not all permutations are local
  • Are there Non-Clifford gates that are useful for distillation?
The most general Bell Permuting gate?
All Clifford gates $\mathcal{C}_n$ on n qubits $$ |\mathcal{C}_n| = 2(4^n-1)4^n|\mathcal{C}_{n-1}| $$
Clifford gates $\mathcal{C}^*_n$ that do not specify phases $$ |\mathcal{C}^*_n| = \frac{1}{4^n}|\mathcal{C}_n| $$
i.e. $\mathcal{C}^*_n = \mathcal{C}_n/\mathcal{P}_n$
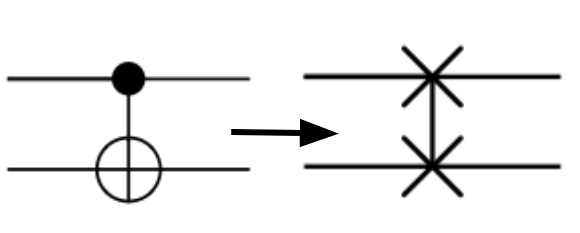
i.e. any $\mathcal{C}_n$ gate can be written as
$C.P\ |\ P\in\mathcal{P}_n\,,C\in\mathcal{C}^*_n$
Bell Preserving (bi-local) gates on n Bell pairs
$$ \mathcal{B}_n $$
$$ \mathcal{B}^*_n = \mathcal{B}_n / \mathcal{P}_n = \mathrm{Sp}(2n, \mathbb{F}_2)$$
$$ \mathcal{B}^*_2 = \mathrm{Sp}(4, \mathbb{F}_2) = \{\underbrace{g}_{\tiny Alice}\otimes \underbrace{g}_{\tiny Bob}\ |\ g\in\mathcal{C}^*_2\}¹²$$
a useful set of cosets: $ Q = \mathcal{C}^*_2 / (\mathcal{C}^*_1 \otimes \mathcal{C}^*_1) $
which provides 20 "distinct" two-qubit gates
  1. Jansen et al.
    Enumerating all bilocal Clifford distillation protocols through symmetry reduction
  2. Dehaene et al.
    Local permutations of products of Bell states and entanglement distillation

Bell Preserving (bi-local) gates on 2 Bell pairs

A $\mathcal{B}_2$ gate can be written as $\underbrace{(g.p)}_{\tiny Alice}\otimes\underbrace{(g)}_{\tiny Bob}$
where $p\in\mathcal{P}_2$
and $g\in\mathcal{C}^*_2$ can be written as $g = g_0.(h\otimes f)$
$h\in\mathcal{C}^*_1$ and $f\in\mathcal{C}^*_1$ and $g_0\in Q$

Bell Preserving (bi-local) gates on 2 Bell pairs

\[ p_1 \in \mathcal{P}_1 \] \[ p_2 \in \mathcal{P}_1 \]
2 Pauli gates
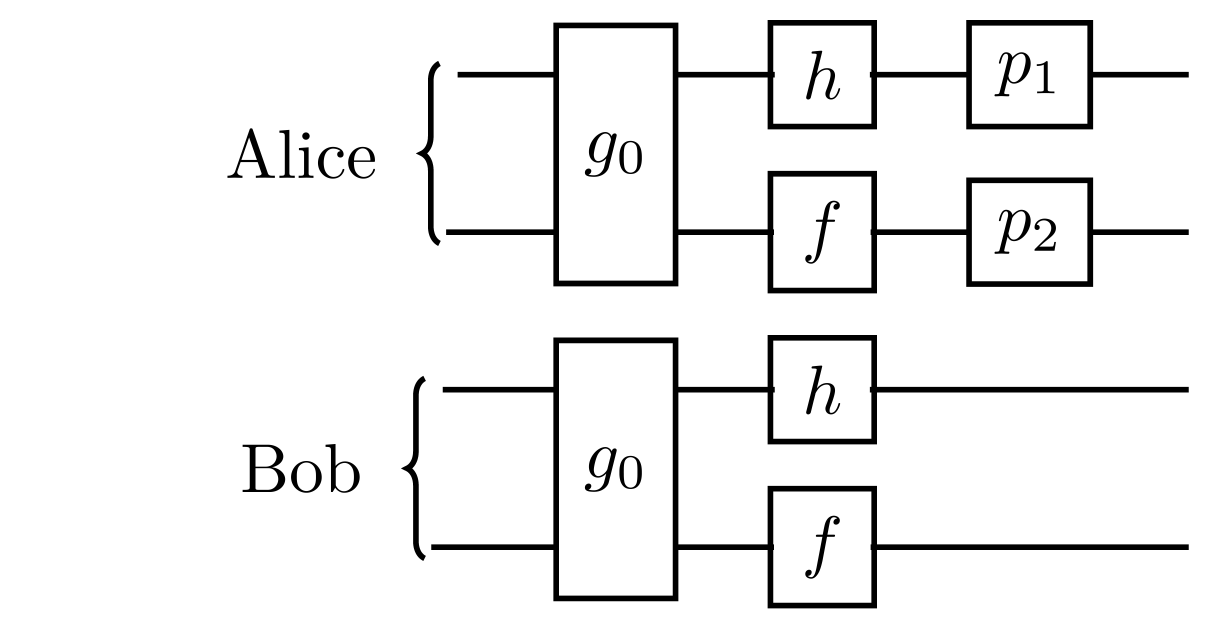
(4 possibilities each)
\[ h\in\mathcal{C}^*_1 \] \[ f\in\mathcal{C}^*_1 \]
2 single-qubit Cliffords
(6 possibilities each)
\[ g_0 \in Q = \mathcal{C}^*_2 / (\mathcal{C}^*_1\otimes\mathcal{C}^*_1) \]
20 "inherently multiqubit" gates
 
20×6×6×4×4 = 720×16 = 11520 different Bell Preserving 2-pair gates
 
 

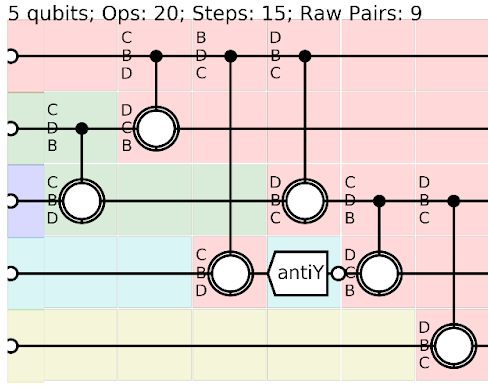
Bell Preserving (bi-local) gates

That also maps AA ⟶ AA
There 720 such gates
But just 36 suffice for state of the art purification...
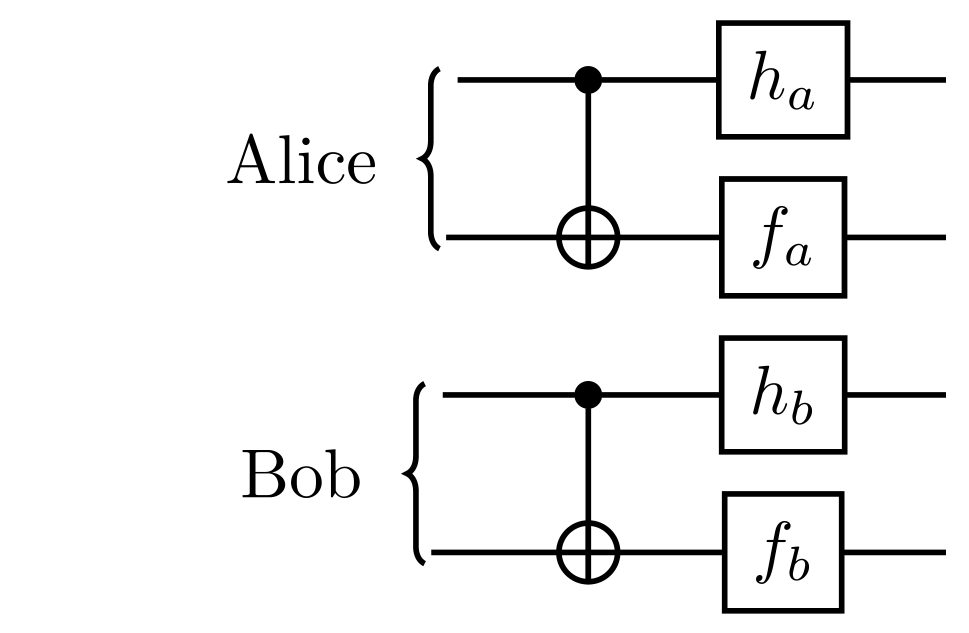
There are 6 possible options for $h_a\otimes h_b$ and $f_a\otimes f_b$ each.
Namely the 6 permutations of BCD.
 
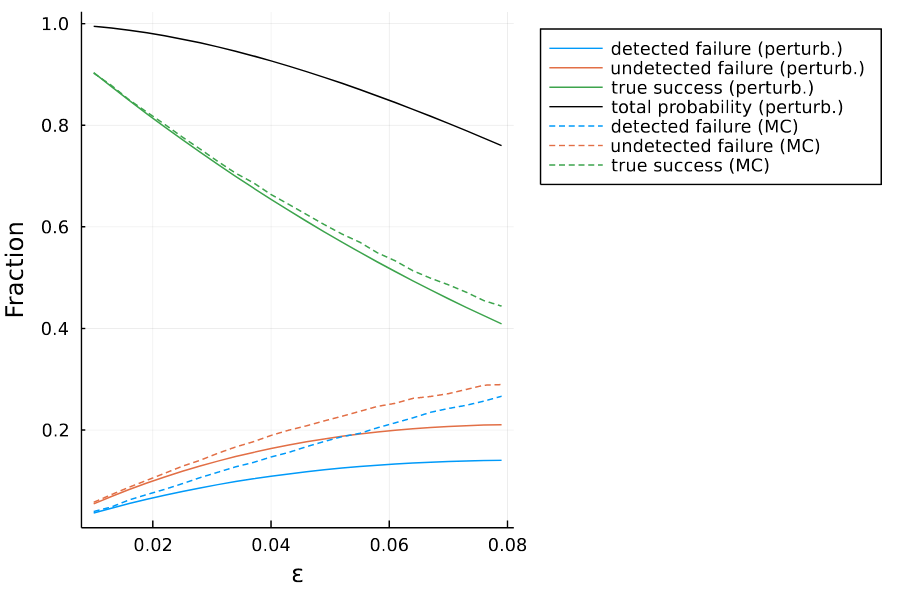
Time to perform a pair of CNOT gates, depending on formalism

Taking Optimization Seriously

Even your Monte Carlo simulations should be "differentiable"!¹
  1. Arya et al.
    Automatic Differentiation of Programs with Discrete Randomness
Monte Carlo vs Perturbative Expansion results.

Full-Stack Design and Optimization Toolkit

Types of Dynamics

Types of Dynamics

Continuous:
Hamiltonians, Master Equations

Types of Dynamics

Continuous:
Hamiltonians, Master Equations
Discrete:
Gates, Circuits

Types of Dynamics

Continuous:
Hamiltonians, Master Equations
Discrete:
Gates, Circuits
Stochastic:
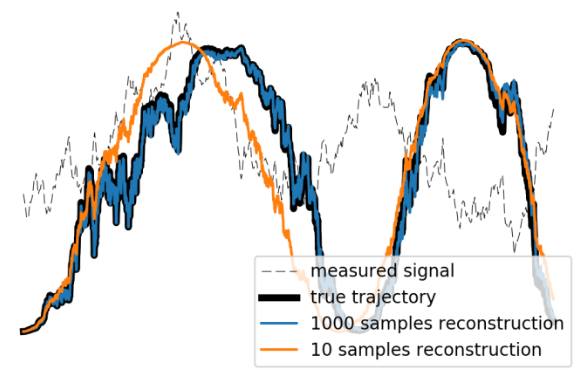
Weak Measurements, Feedback

State Representation

Kets and density matrices
Tableaux and graphs
Matrix product states and tensor network states

                traits = [Qubit(), Qubit(), Qumode()]
                reg = Register(traits)

A register "stores" the states being simulated.


                graph = grid([2,3])
                registers = [...]
                net = RegisterNet(graph, registers)

A "graph" of registers can represent a network.


                initialize!(reg[1], X₁)

A register's slot can be initialized to an arbitrary state, e.g. $|x_1\rangle$ an eigenstate of $\hat{\sigma}_x$.


                initialize!(reg[1], X₁)
                initialize!(reg[2], Z₁)
                apply!((reg[1], reg[2]), CNOT)

Arbitrary quantum gates or channels can be applied.


              project_traceout!(reg[1], σˣ) # Projective measurement

              observable((reg[1],reg[2]), σᶻ⊗σˣ) # Calculate an expectation

Measurements and expectation values...

Full Symbolic Computer Algebra System


              julia> Z₁
              |Z₁⟩
            

              julia> ( Z₁⊗X₂+Y₁⊗Y₁ ) / √2
              0.707 (|Y₁⟩|Y₁⟩+|Z₁⟩|X₂⟩)

Symbolic to Numeric Conversion


              julia> express( ( Z₁⊗X₂+Y₁⊗Y₁ ) / √2 )
              Ket(dim=4)
                basis: [Spin(1/2) ⊗ Spin(1/2)]
                 0.8535533905932736 + 0.0im
                                0.0 + 0.3535533905932737im
               -0.49999999999999994 + 0.3535533905932737im
                -0.3535533905932737 + 0.0im
            

              julia> express( Y₁⊗Y₂, CliffordRepr() )
              Rank 2 stabilizer
              + Z_
              + _Z
              ════
              + Y_
              - _Y
              ════
Full repeater sim with automatic instrumentation.

              for (;src, dst) in edges(mgraph)
                  @process entangler(sim, mgraph, src, dst, ...)
              end
              for node in vertices(mgraph)
                  @process swapper(sim, mgraph, node, ...)
              end
              for (;src, dst) in all_node_pairs(mgraph)
                  @process entangler(sim, mgraph, src, dst, ...)
              end

Automatic tracking of noise processes


                reg = Register([Qubit(), Qubit(), Qubit()])
              

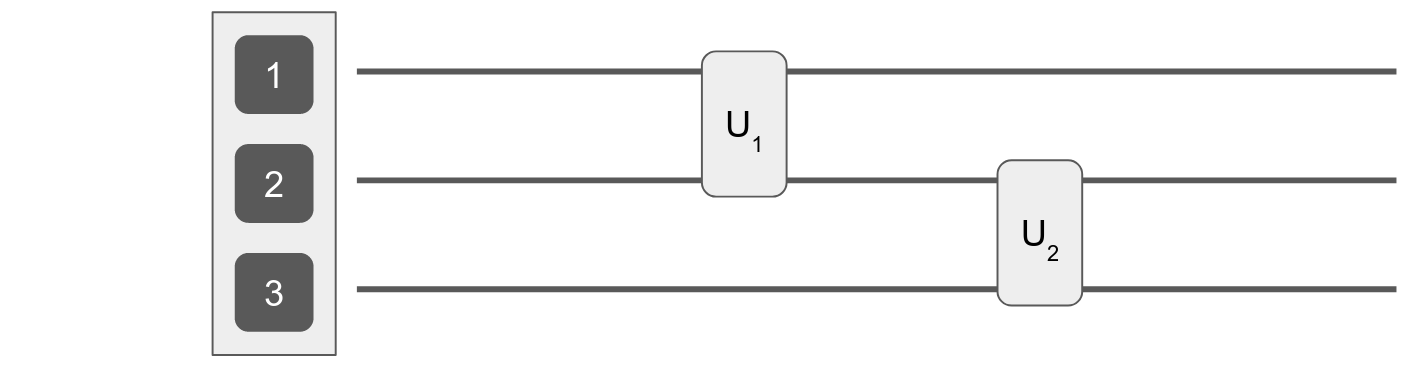
                reg = Register(
                  [Qubit(), Qubit(), Qubit()]
                  [T1Decay(T₁), CoherentError(ε*σᶻ), NZ(...)]
                )
              

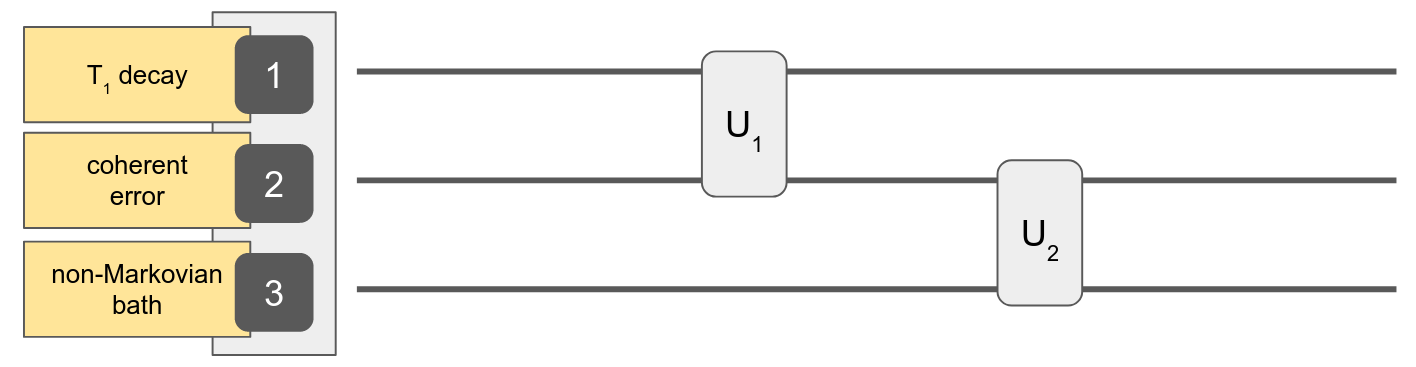
                reg = Register(
                  [Qubit(), Qubit(), Qubit()]
                  [T1Decay(T₁), CoherentError(ε*σᶻ), NZ(...)]
                )
                apply!((reg[1],reg[2]), CNOT; time=τ₁)
              

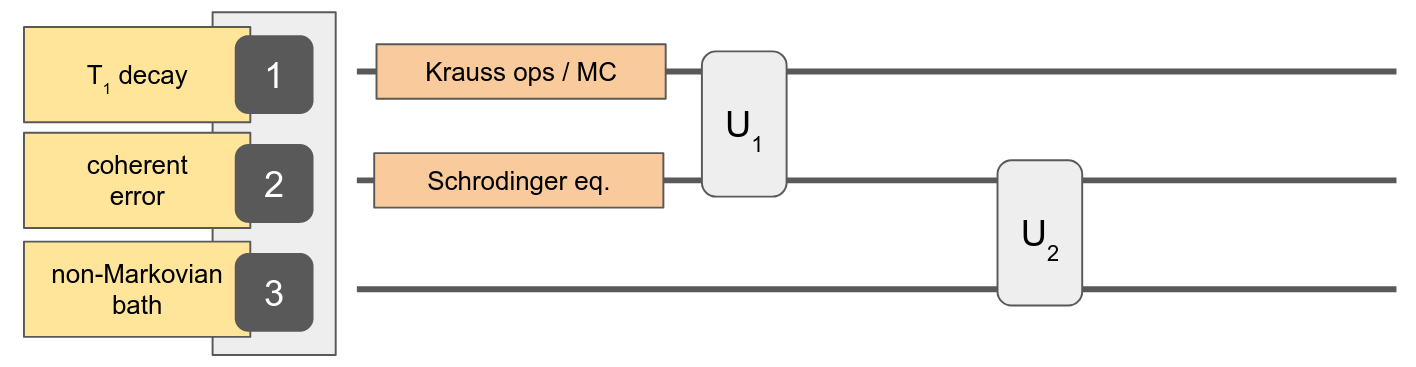
                reg = Register(
                  [Qubit(), Qubit(), Qubit()]
                  [T1Decay(T₁), CoherentError(ε*σᶻ), NZ(...)]
                )
                apply!((reg[1],reg[2]), CNOT; time=τ₁)
                apply!((reg[2],reg[3]), CPHASE; time=τ₂)

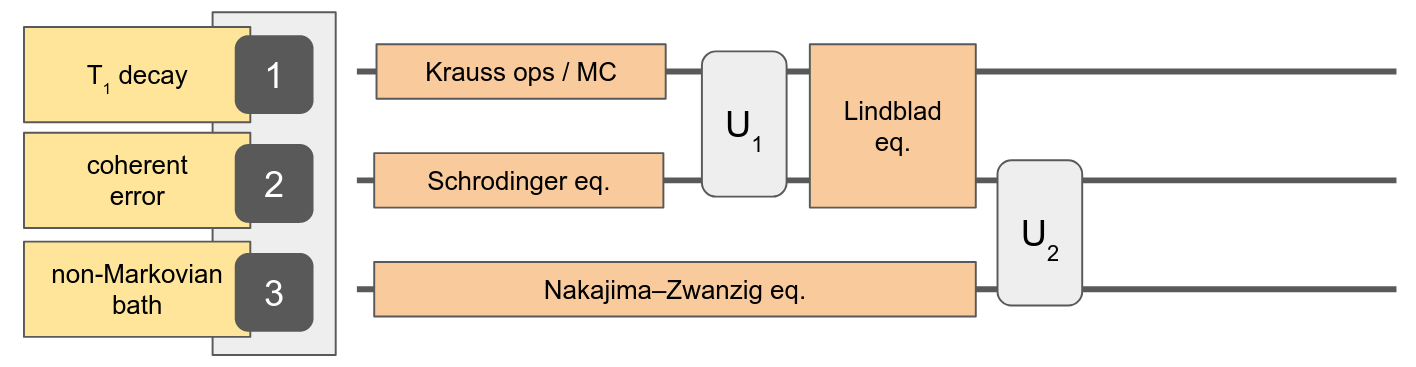
Other features...

Declarative specification of "imperfections"

Discrete event scheduling

Traveling wavepackets modeling

More formalisms

More symbolic algebra

Digital twin / surrogate modeling

QuantumSavory.jl

github.com/Krastanov/QuantumSavory.jl

Better modeling and better optimization for entanglement exist

Try out QuantumClifford.jl - it is public and stable

Be an early tester for QuantumSavory.jl

 

Including work done by Vaishnavi Addala and Shu Ge, in coordination with Dirk Englund.

Consider gradschool or postdoc at UMass Amherst:

Design of optical/mechanical/spin devices with Sandia, Mitre, and MIT.

Working on practical LDPC ECC in networking and computing.

Creating new tools for the entire community.