All-Photonic Artificial Neural Network Processor Via Non-linear Optics
Stefan Krastanov | MIT ⟶ UMass Amherst work by Basani, Heuck, Englund, KrastanovRoom-Temperature Optical Quantum Computing
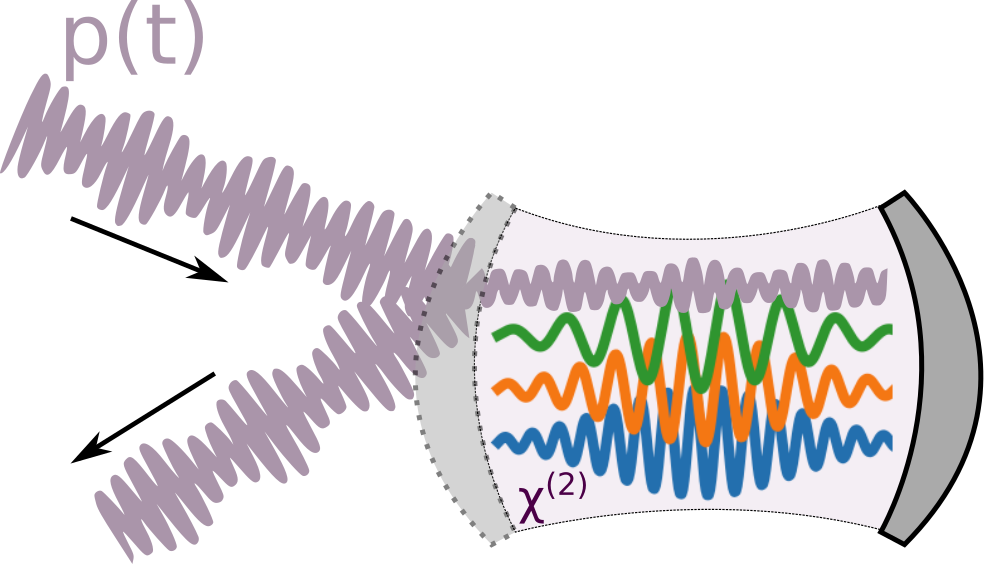
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities

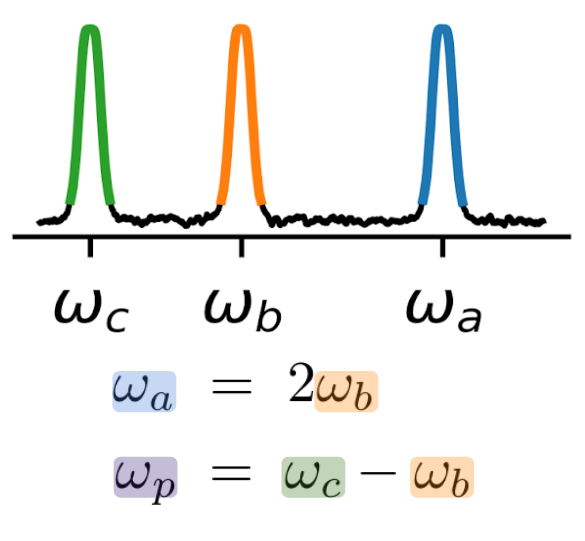
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities


- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities


A rather "poor" Hamiltonian...
- Krastanov et al.Room-temperature photonic logical qubits via second-order nonlinearities
Can be twisted into something useful:
Can be twisted into something useful:
Full error correction
Can be twisted into something useful:
Full error correction
Can be twisted into something useful:
Full error correction
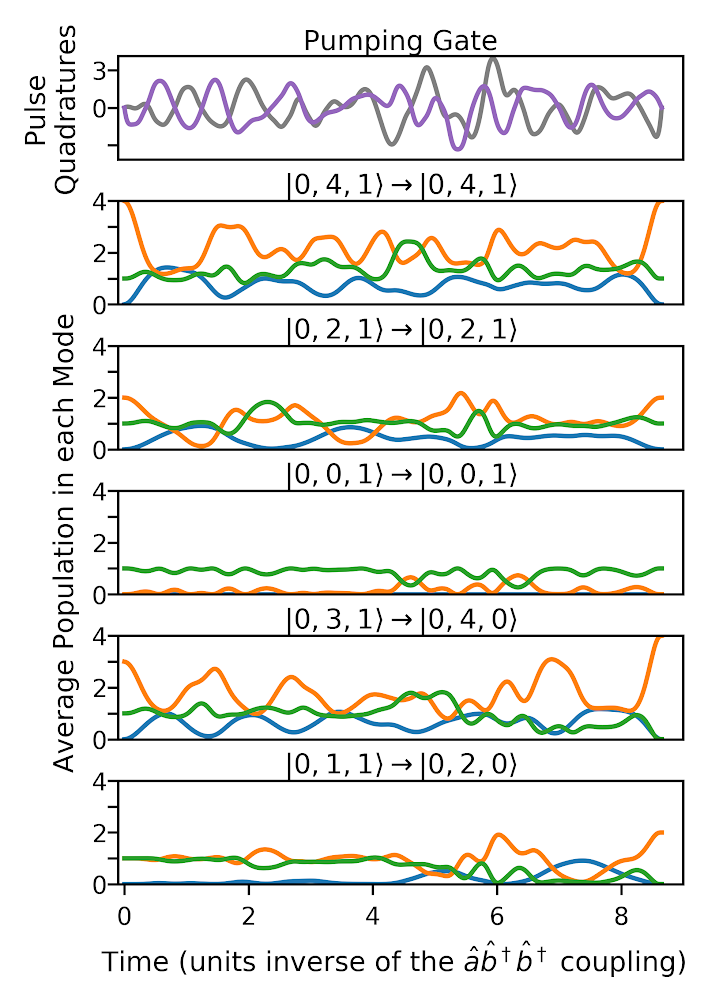
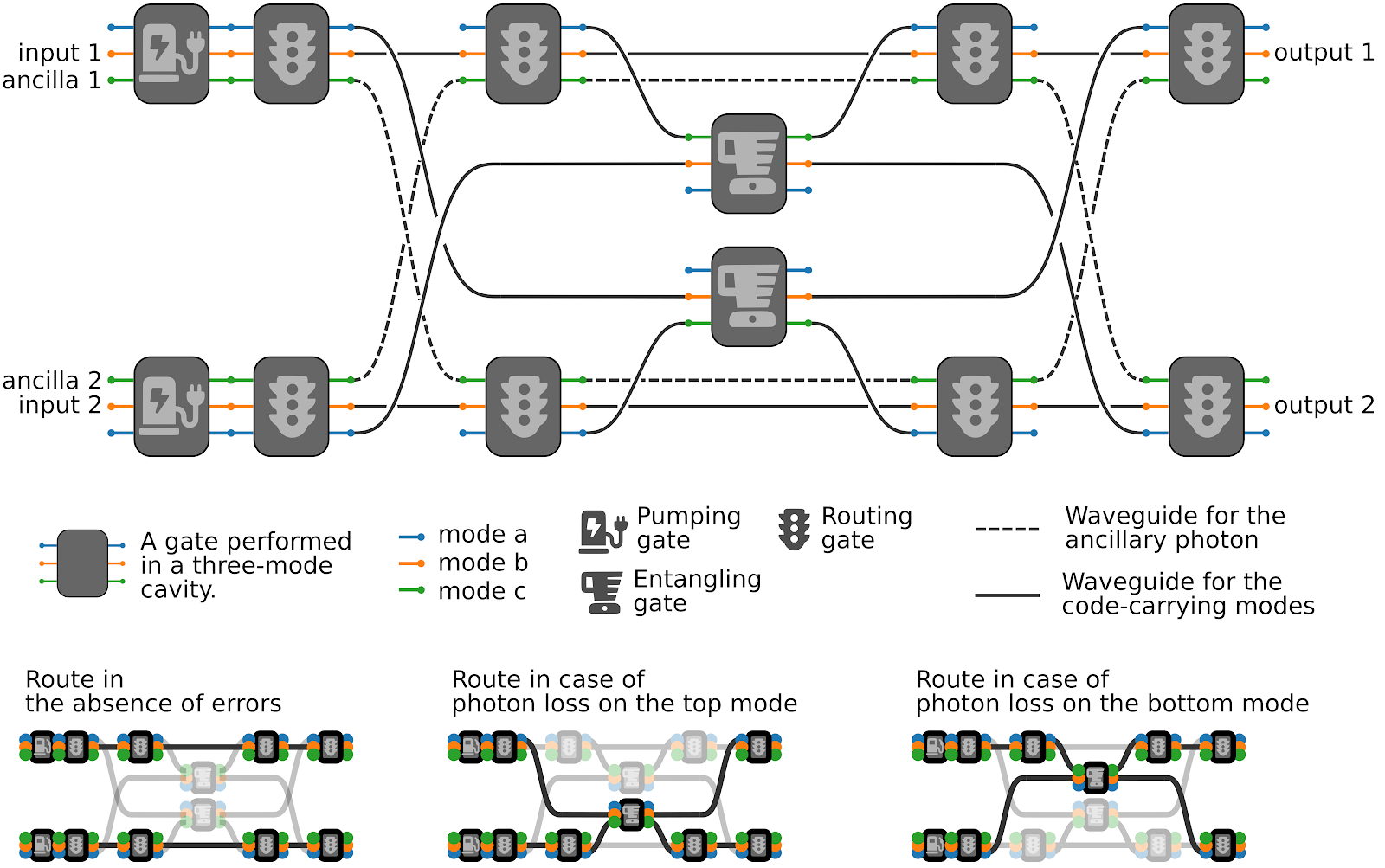
Is this a realistic device?
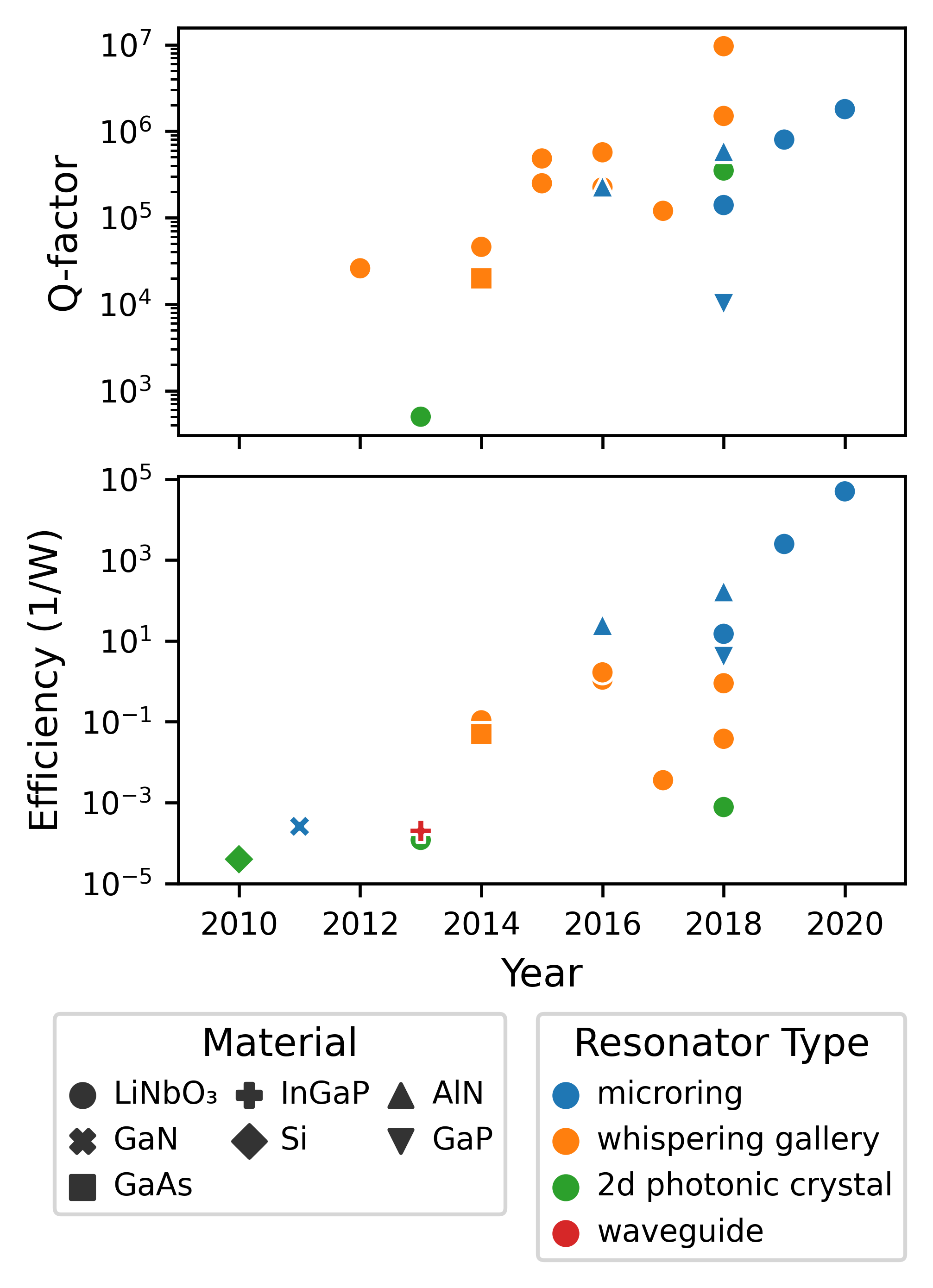
All-photonic Linear Algebra Accelerator Via Non-linear Optics
All-to-all neuron interactions in a single on-chip component
Reversible computation
Interesting performance-power relationship
The "Computational Core"
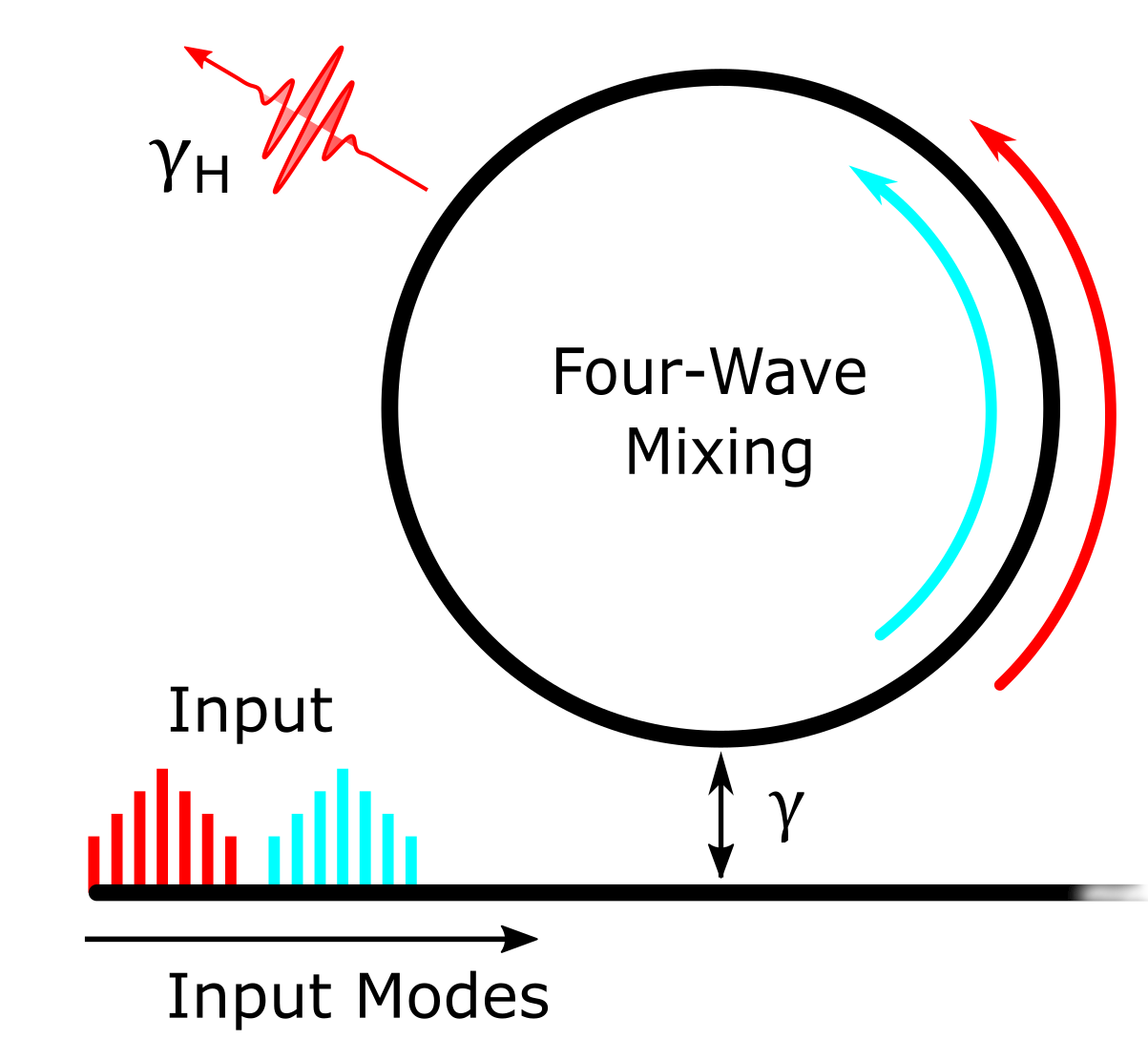

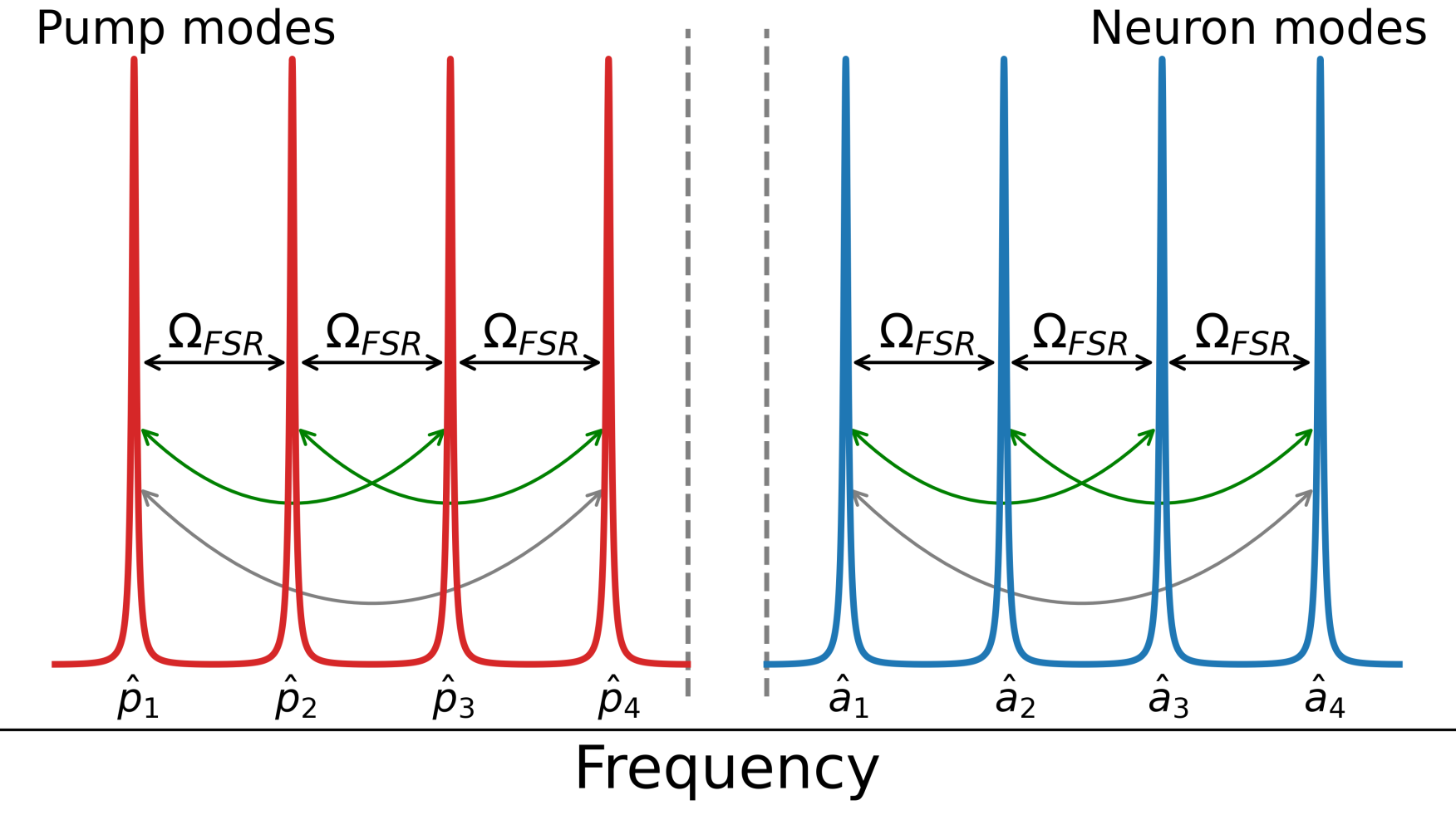
System dynamics
Where \(A_\dots\) stands for "neural amplitudes"
and \(P_\dots\) stands for "pump amplitudes".
\(P_1\gg P_i\) is a convenient simplification, but unimportant
Simplifying Assumptions and Hardware alternatives
We assumed strong pumps to avoid neural Kerr
- ... but we could have forgone linearity
- ... maybe also assume in-situ training
- ... or switch to \(\chi^{(2)}\) media
- ... but that would require orders of magnitude difference in pump and neuron frequencies
Effective dynamics - matrix multiplication
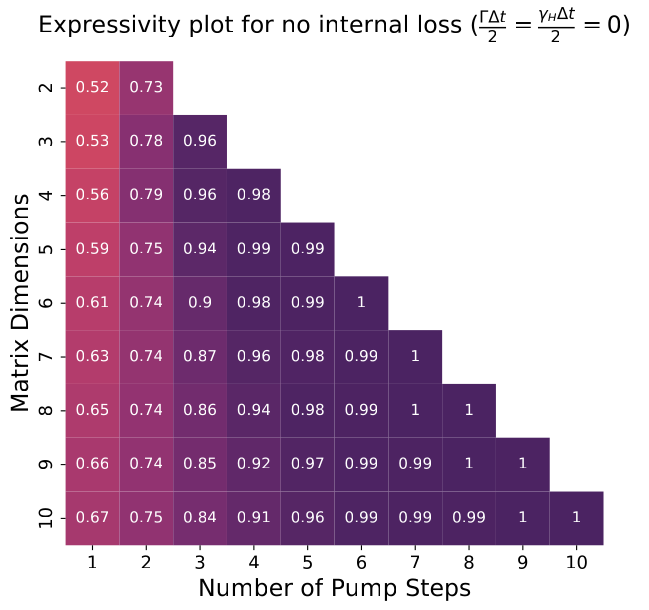
Expressivity
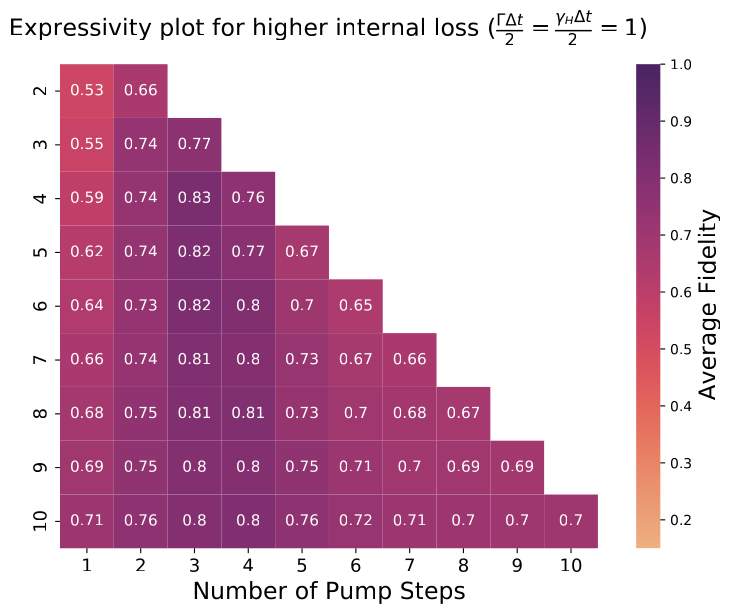
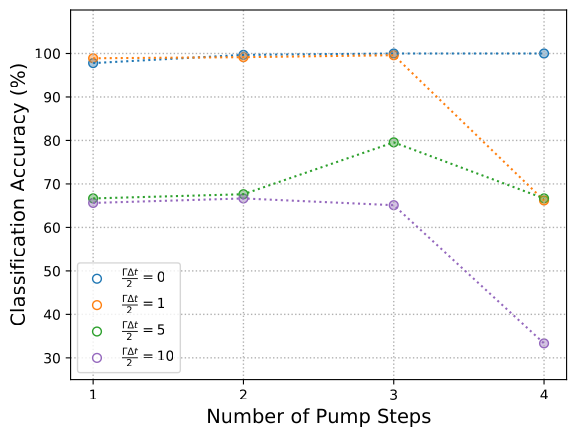
Linear classification example
Activation Function
sigmoid
nonlinearity
Fully optical implementation
capable of working with negative (or complex) numbersArchitecture
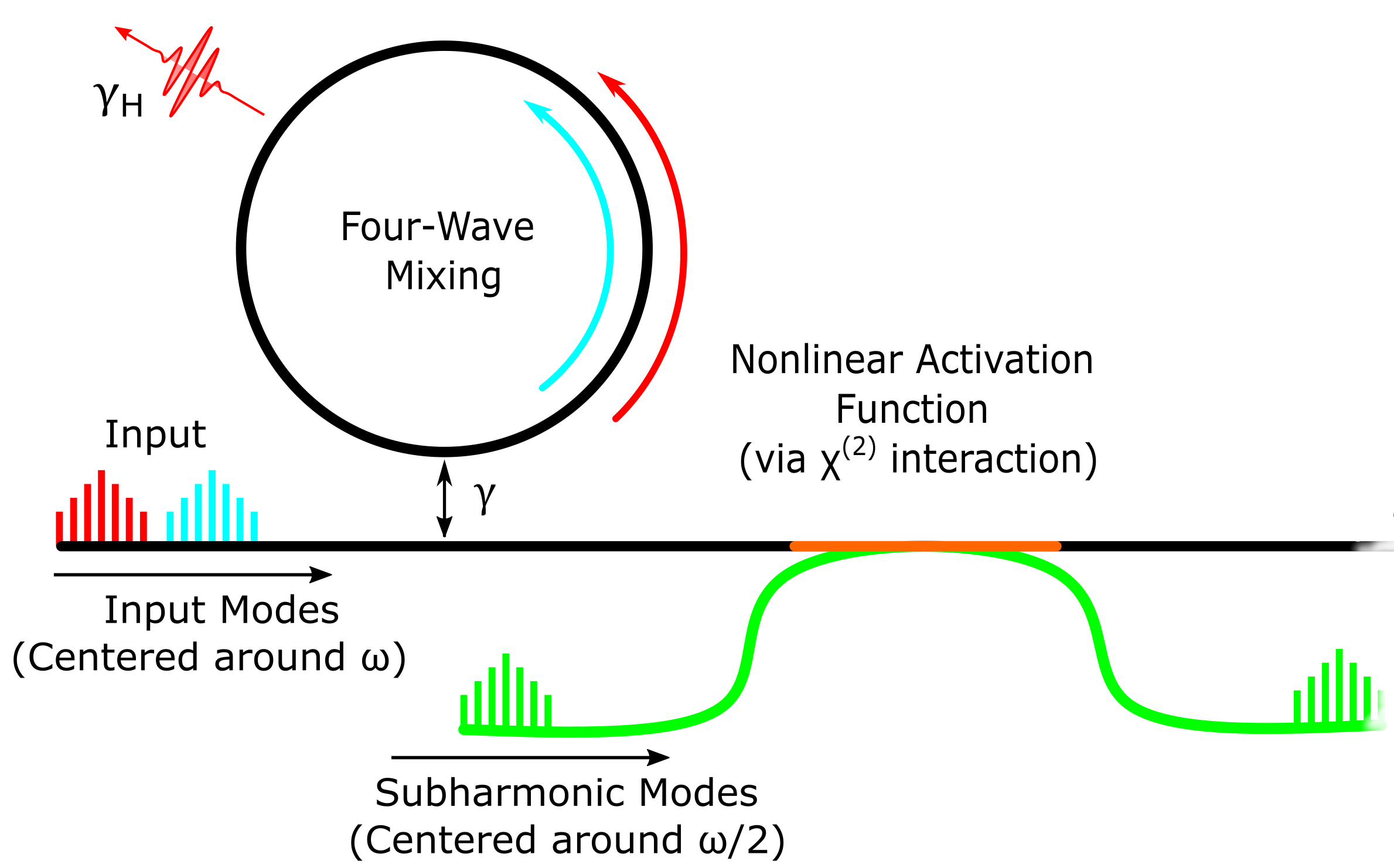
System dynamics
Interactive supplementary materials at pluto.krastanov.org.
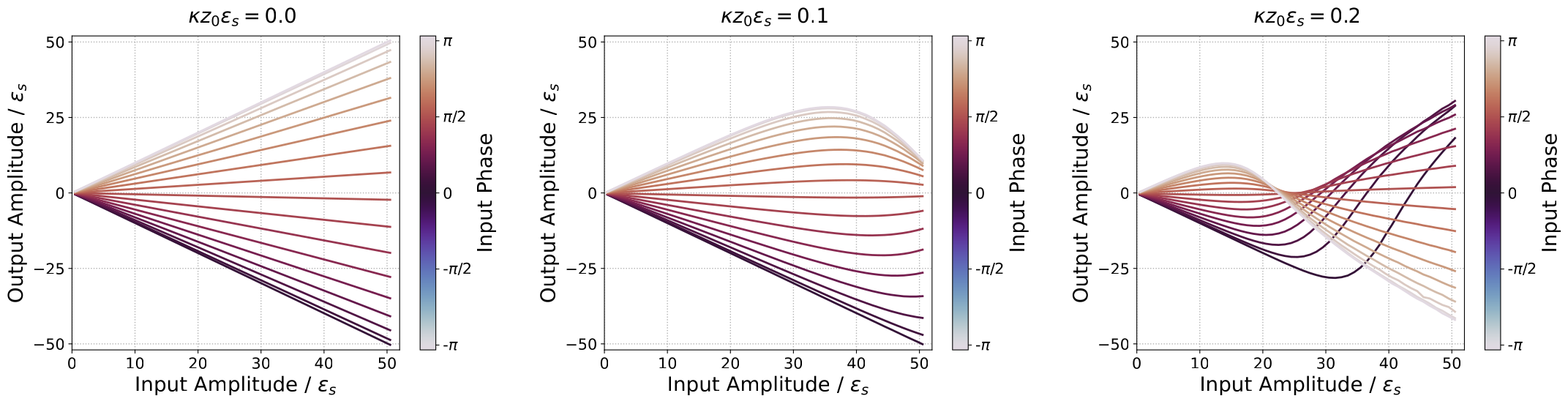
(Nonlinear) Amplification
A Case Study
Digit recognition with MNIST
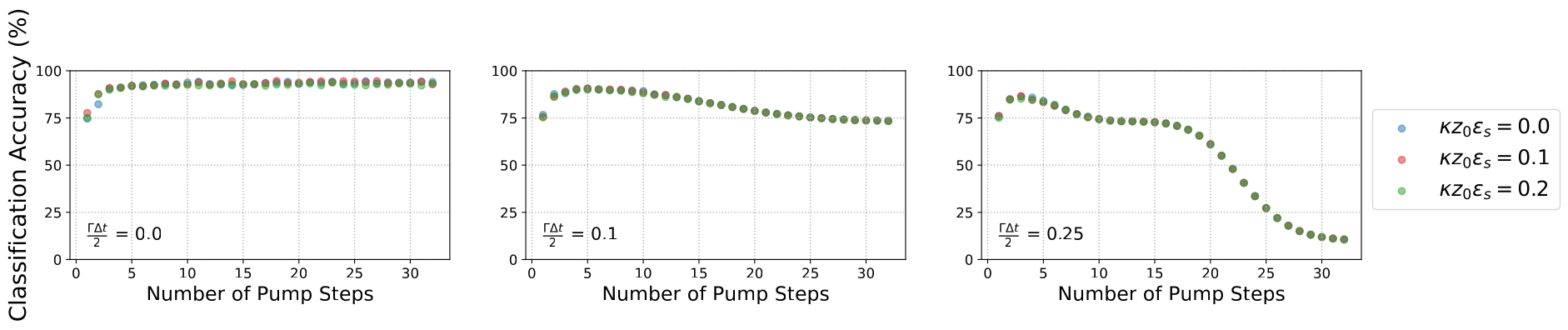
Main Takeaways
All-to-all neuron interactions in a single on-chip component.
Self-funded dev program for room-temperature quantum computing.
Consider a postdoc at UMass Amherst:

Design of optical/mechanical/spin devices with Sandia, Mitre, and MIT.
Creating new modeling tools for the entire community.