Stochastic Estimation of Dynamical Variables

Stefan Krastanov1, Sisi Zhou1, Steven T. Flammia1,2, Liang Jiang1

1Yale Quantum Institute, Yale University, New Haven, Connecticut 06520, USA

2Centre for Engineered Quantum Systems, School of Physics, University of Sydney, Sydney NSW, Australia

Abstract

Estimating the parameters governing the dynamics of a system is a prerequisite for its optimal control. We present a simple but powerful method that we call STEADY, for STochastic Estimation Algorithm for DYnamical variables, to estimate the Hamiltonian (or Lindbladian) governing a quantum system.

STEADY makes efficient use of all measurements and its performance scales as the information-theoretic limits for such an estimator. Importantly, it is inherently robust to state preparation and measurement errors. It is not limited to evaluating only a fixed set of possible gates, rather it estimates the complete Hamiltonian of the system. The estimator is applicable to any Hamiltonian that can be written as a piecewise-differentiable function and it can easily include estimators for the non-unitary parameters as well.

At the heart of our approach is a stochastic gradient descent over the difference between experimental measurement and model prediction.

Learning a Model of the Hardware

A quantum system is controlled by a Hamiltonian $H(\boldsymbol{d})$, that is itself a function of time-dependent control pulse $\boldsymbol{d}(t)$, a $D$-dimensional real vector set by the experimentalist.

To accurately predict this dynamics we must learn the Hamiltonian $H$. We introduce a richly parameterized model for the Hamiltonian, $\tilde{H}(\boldsymbol{\omega};\boldsymbol{d})$, in which case the problem becomes finding the values of all parameters in the array $\boldsymbol{\omega_{0}}$ for which $H(\boldsymbol{d})=\tilde{H}(\boldsymbol{\omega_{0}};\boldsymbol{d})$ for all $\boldsymbol{d}$.

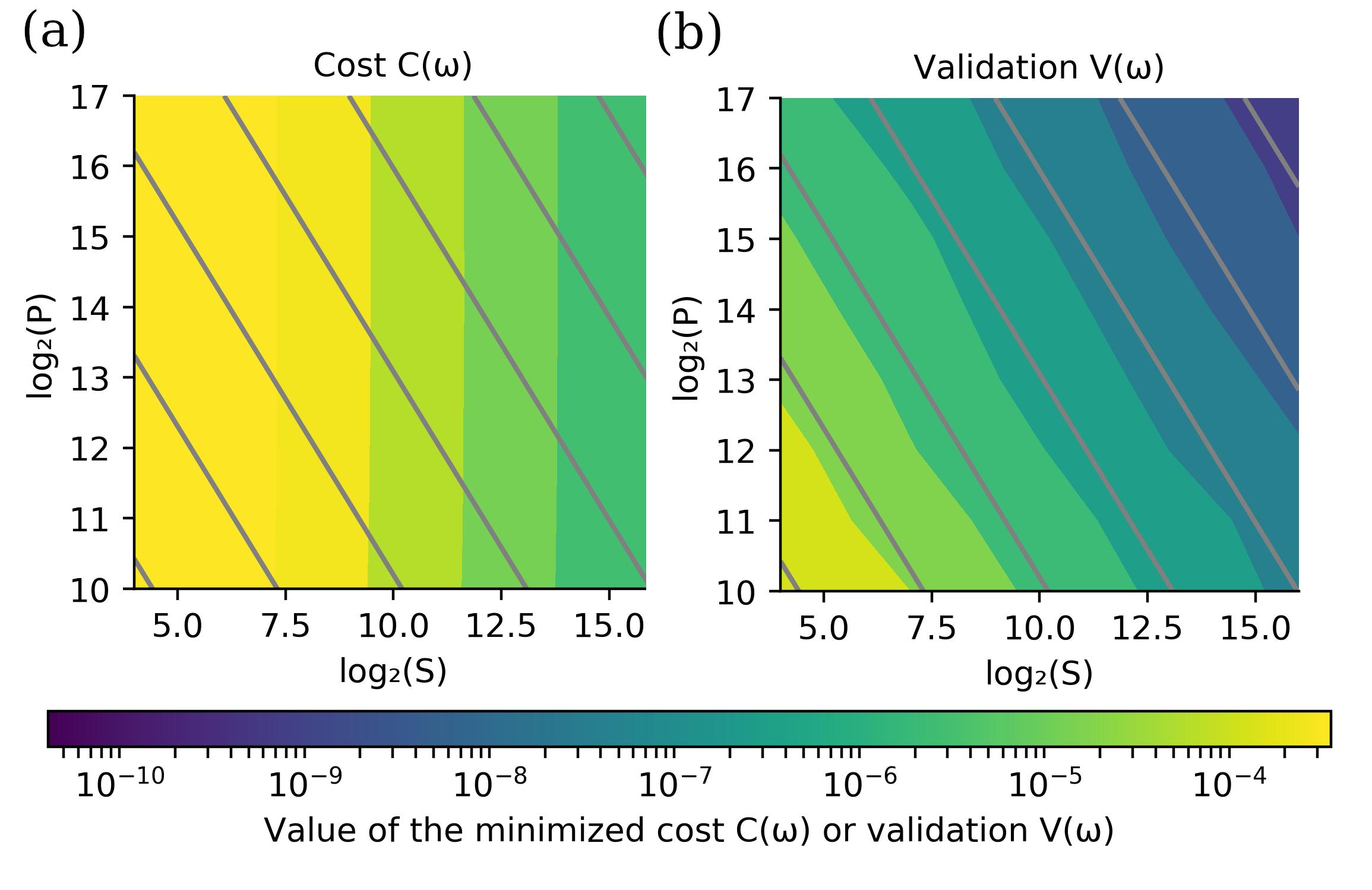
We can define the "distance" between the measured estimate for the population $\hat{\boldsymbol{p}}$ and the predicted population $\tilde{\boldsymbol{p}}_{i}(\boldsymbol{\omega})$, averaged over the $P$ random pulses: $$ C(\boldsymbol{\omega})=\frac{1}{P}\sum_{i=1}^{P}\text{dist}\left(\hat{\boldsymbol{p}}_{i},\tilde{\boldsymbol{p}}_{i}(\boldsymbol{\omega})\right). $$ Our estimator $\hat{\boldsymbol{\omega}}$ for $\boldsymbol{\omega_{0}}$ is the minimum of this distance measure (i.e. cost function): $$ \hat{\boldsymbol{\omega}}=\arg\min_{\boldsymbol{\omega}} C(\boldsymbol{\omega}). $$

An example of very general parameterization is $\tilde{H}_{ij}(\boldsymbol{\sigma},\boldsymbol{h};\boldsymbol{d})=h_{ij}+\sum_{k=1}^{D}\sigma_{ijk}d_{k}$.

A pictorial representation of the STEADY parameter estimation protocol. We sample the behavior of the hardware under calibration for a set of randomly chosen control drives and compare it to the prediction of a parameterized model. Through a stochastic gradient descent we find the parameter values that minimize the difference between model prediction and experimental result, repeating steps 4 and 5 at each iteration of the gradient descent.

Estimator Performance and
Information Theory Bounds

The fidelity of our estimator increases steadily with more measurement data, scaling as the Cramér-Rao bound from Information Theory. The performance is not limited by the uncertainty (due to finite sampling) in the population measurements. Compare (a) the minimized cost function $ C(\boldsymbol \omega) $ and (b) the minimized validation function $ V(\boldsymbol{\omega})= \frac{1}{P_{v}}\sum_{i=1}^{P_{v}}\text{dist}\left( \boldsymbol{p}_{i}, \tilde{\boldsymbol{p}}_{i}\left(\boldsymbol{\omega}\right) \right)$, where $\boldsymbol{p}_{i}$ is the exact population. The horizontal axis gives the number of samples $S$ taken per pulse, while the vertical axis gives the number of unique random pulses $ P $ used. The scales are binary logarithmic (i.e. $10$ corresponds to $ 2^{10} $ samples or pulses). The gray lines show constant $ P\times S $ (and they are logarithmically spaced). The color map is logarithmic as well.

Conclusions and Outlook

STEADY reaches the information-theoretic performance limits. The method is inherently insensitive to general SPAM errors plaguing approaches like process tomography. Working at the Hamiltonian/Lindbladian level gives us greater control than what methods restricted to sets of pre-compiled gates provide, letting us use optimal control techniques when manipulating the system. We have used this versatility to enable well known techniques like D-optimal experimental design to further improve the fidelity of our estimator.

Krastanov et al., "Stochastic Estimation of Dynamical Variables", Quantum Science and Technology, 2019, (arXiv:1812.05120)