I'll be your qubit

Interactive immersive installation where the viewer is introduced to the experience of the quantum world.

Stefan Krastanov1, Florian Carle1, Michel Devoret1, Martha W. Lewis1,2

1Yale Quantum Institute, Yale University, New Haven, Connecticut 06520, USA; 2Erector Square LLC, New Haven, Connecticut 06513, USA

Introduction

The behavior humanity has observed in quantum systems has confounded the everyday intuition of the human observers for more than a century now. Considerable effort has been spent on trying to reframe this weird behavior in terms of less "spooky", classical theories of "hidden variables". However, evidence from both experiments and purely mathematical constructs have shown that the only path free of contradictions is embracing that reality can only be quantum.

I'll be your qubit! provides for a personalized experience of the contradictions that quell any attempt to explain the rich quantum world in terms of noncontextual hidden variable theories. The installation's ceiling diagram is described on the right and below we describe richer resources that the interested might want to look up.

The I'll be your qubit ceiling diagram

The ceiling diagram shows a graph representation of a subset of the Pauli group of two qubits. Each vertex is an operator. Edges connect operators that commute with each other, i.e. operators that are compatible observables. Each edge corresponds to a complete set of commuting observables. Moreover, there are 9 cycles of length 3, corresponding to sets of 3 compatible observables. These sets are overdetermined and have their total parity constrained. Cycles of parity 1 are depicted as blue while cycles of parity -1 are red. This diagram is a variation of the Mermin-Peres square, one of the tools used to exemplify the infeasibility of hidden variable theories.

Kochen–Specker theorem

Noncontextual hidden variable theories require that all hidden variables corresponding to observables have definite values, and that the values of those variables are independent of the measurement device. The two requirements are contradictory due to the non-commutativity of quantum mechanical observables [1-3]. The constructs on the right can be used in the proof.

Mermin-Peres magic square

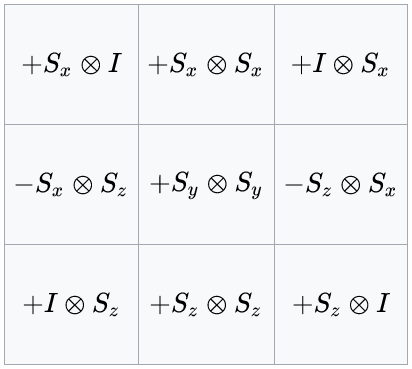
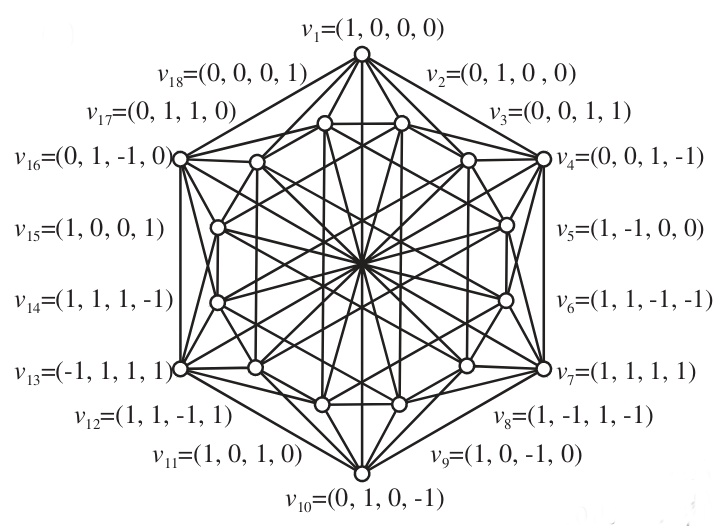
Each row and each column contains a mutually commuting set of observables with eigenvalues +1 and −1. The product of the observables in each row is the identity operator, and the product of observables in each column equates to minus the identity operator [2,4].

Cabello graphs

To any correlation experiment, we can associate a graph in which events are represented by vertices and pairs of exclusive events are represented by adjacent vertice. This is one of the most powerful ways to prove the Kochen-Specker theorem and other non-contextuality inequalities like Bell's inequality [5,6]. This graph formalism is the inspiration for the simplified visualization in "I'll be your qubit!".

References

For more of Martha's work:
marthalewis.com, Martha W. Lewis.
[1]: Kochen–Specker theorem. In Wikipedia, The Free Encyclopedia
[2]: Peres, A. (1991). Two simple proofs of the Kochen-Specker theorem. Journal of Physics A: Mathematical and General, 24(4), L175.
[3]: Cabello, A., Estebaranz, J., & García-Alcaine, G. (1996). Bell-Kochen-Specker theorem: A proof with 18 vectors. Physics Letters A, 212(4), 183-187.
[4]: Quantum pseudo-telepathy. In Wikipedia, The Free Encyclopedia
[5]: D’Ambrosio, V., Herbauts, I., Amselem, E., Nagali, E., Bourennane, M., Sciarrino, F., & Cabello, A. (2013). Experimental implementation of a Kochen-Specker set of quantum tests. Physical Review X, 3(1), 011012.
[6]: Cabello, A., Severini, S., & Winter, A. (2014). Graph-theoretic approach to quantum correlations. Physical review letters, 112(4), 040401.