Outline

• A New Phase-rotation Gate for a Cavity-Qubit System
• Performing Arbitrary Unitary Operations on the Cavity

The System

Cavity (oscillator) coupled to a qubit (a two-level system)

\(\hat{H}_{0}=\omega_{q}\mid e\rangle\langle e\mid+\omega_{c}\hat{n}-\chi\mid e\rangle\langle e\mid \hat{n}\)

The System

Cavity (oscillator) coupled to a qubit (a two-level system)

\(\hat{H}_{0}=\color{red}{\omega_{q}\mid e\rangle\langle e\mid}+\omega_{c}\hat{n}-\chi\mid e\rangle\langle e\mid \hat{n}\)

The System

Cavity (oscillator) coupled to a qubit (a two-level system)

\(\hat{H}_{0}=\omega_{q}\mid e\rangle\langle e\mid+\color{red}{\omega_{c}\hat{n}}-\chi\mid e\rangle\langle e\mid \hat{n}\)

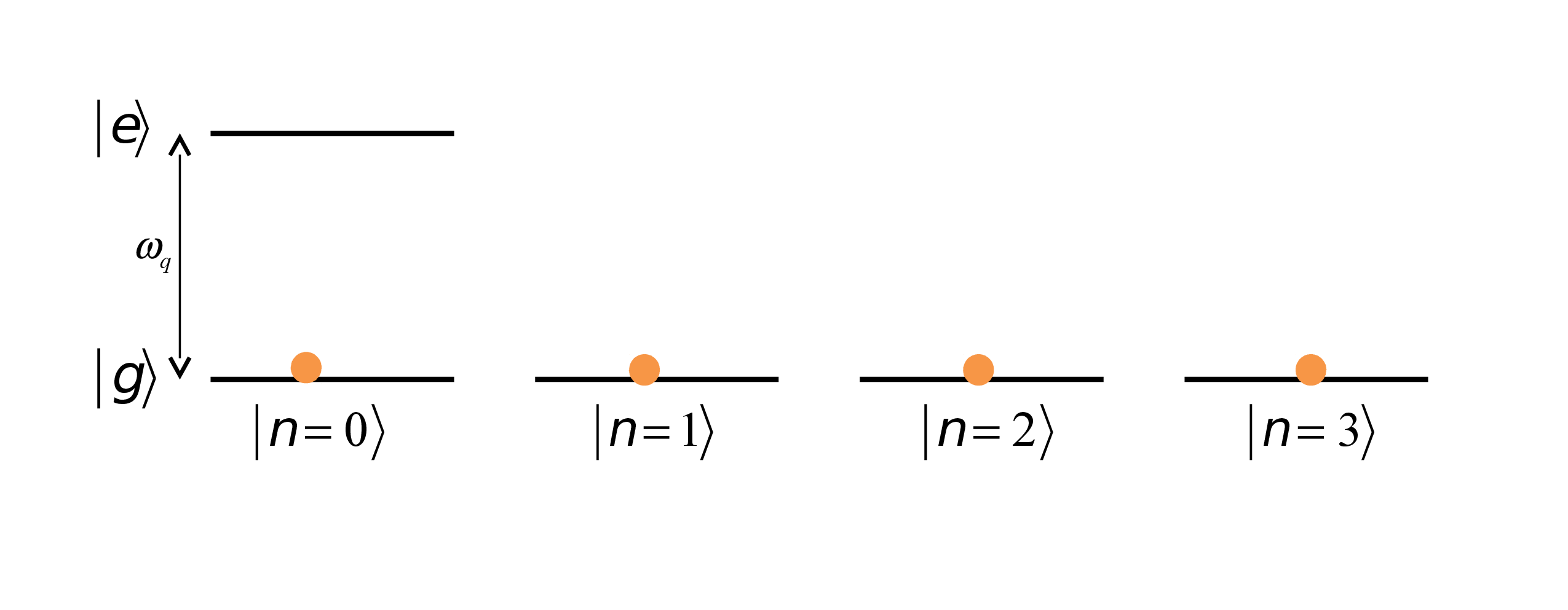
The System

Cavity (oscillator) coupled to a qubit (a two-level system)

\(\hat{H}_{0}=\omega_{q}\mid e\rangle\langle e\mid+\omega_{c}\hat{n}-\color{red}{\chi\mid e\rangle\langle e\mid \hat{n}}\)

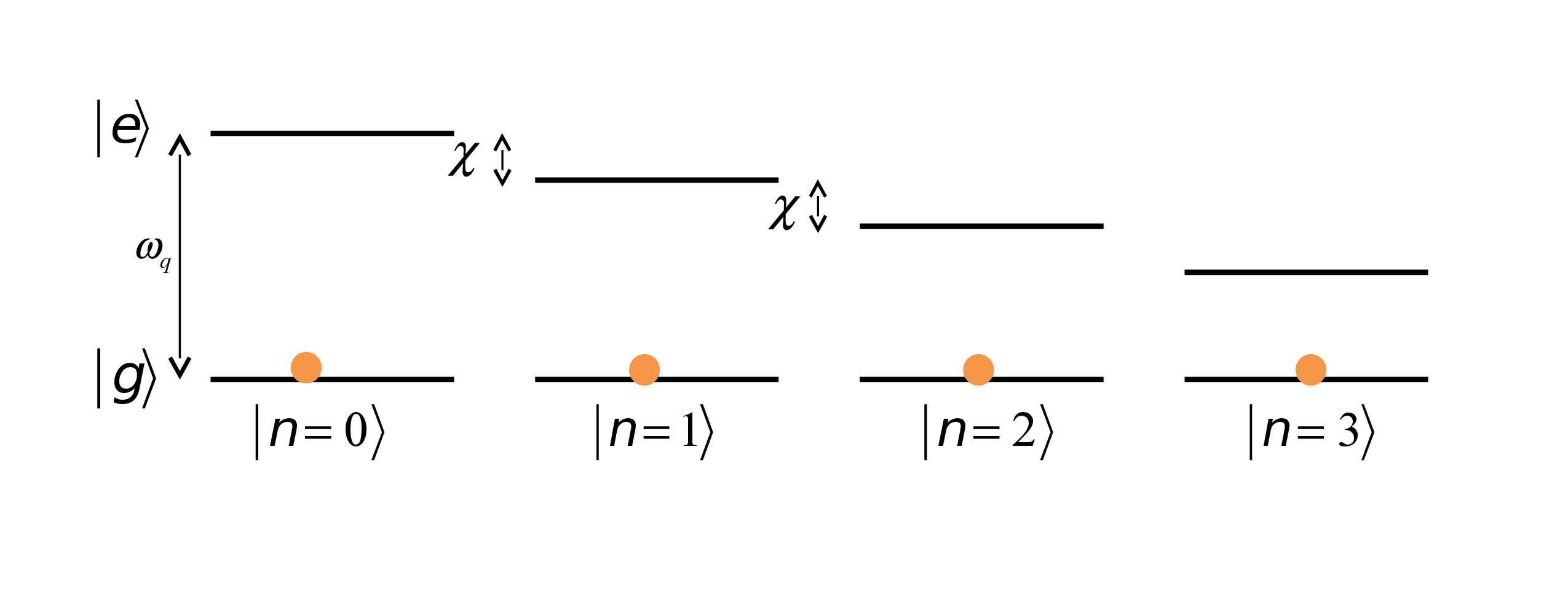
The Drives - Controlling the Cavity

\(\hat{H}_{cavity}=\varepsilon\left(t\right)e^{i\omega_{c}t}\hat{a}^{\dagger}+h.c.\)

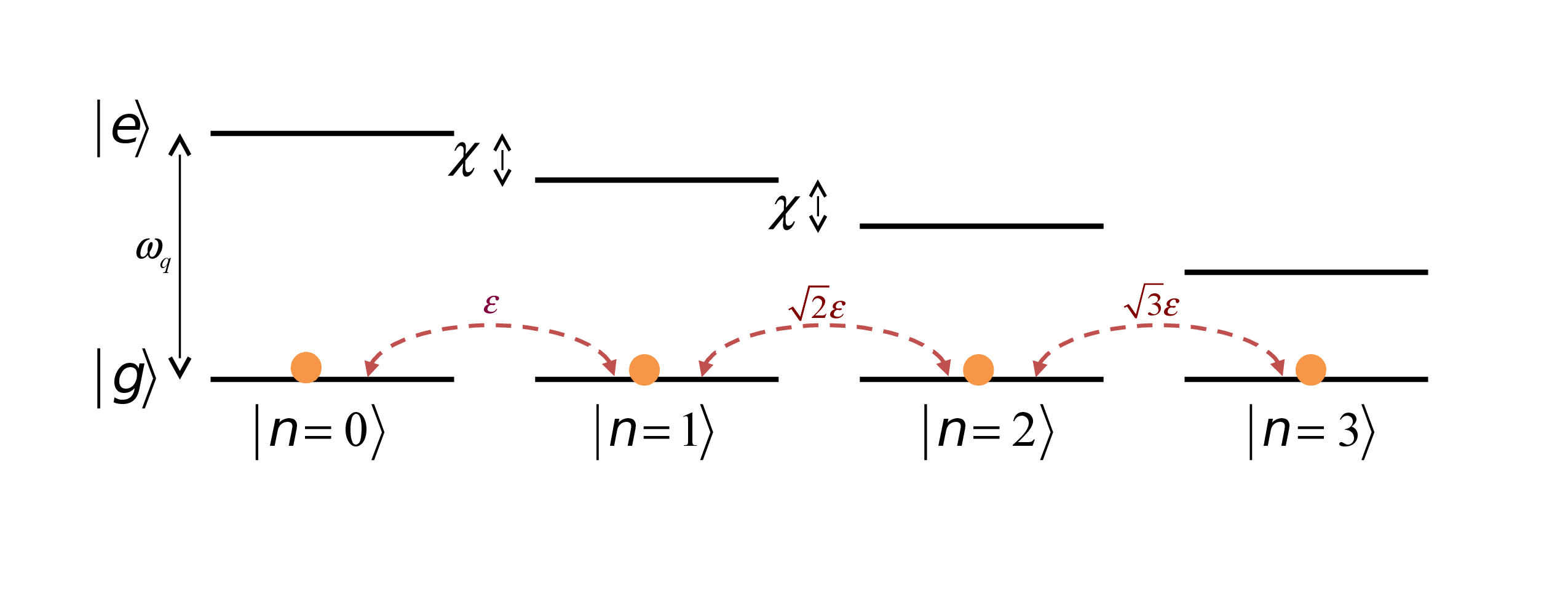
The Drives - Controlling the Qubit

\(\hat{H}_{qubit}=\Omega\left(t\right)e^{i\omega_{q}t}\left|e\rangle\langle g\right|+h.c.\)

Selective on the number of photons: \(\Omega(t) = \Omega e^{-in\chi t}\) with \(\Omega\ll\chi\)

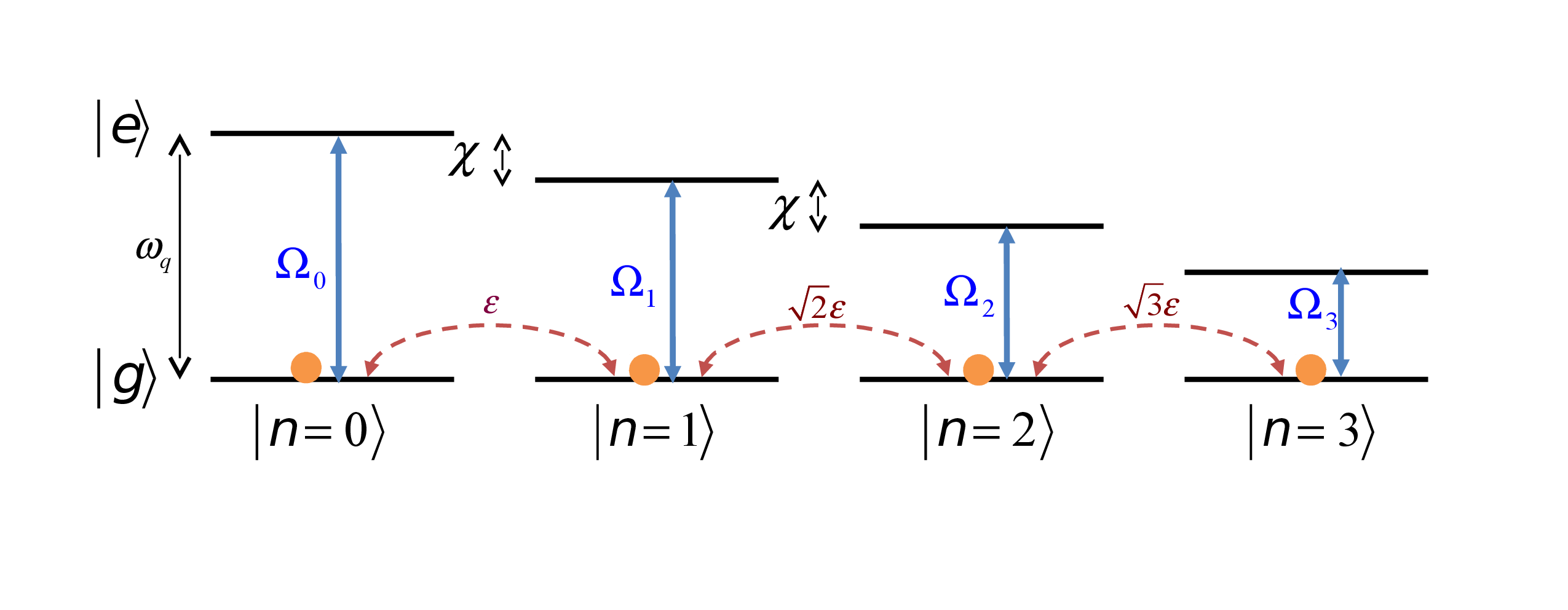
"SNAP" Gate

Selective on Number Arbitrary Phase \(\left|g,n\right\rangle \rightarrow e^{i\theta_{n}}\left|g,n\right\rangle\)

\(\hat{S}_{n}\left(\theta_{n}\right)=e^{i\theta_{n}\left|n\rangle\langle n\right|}\)

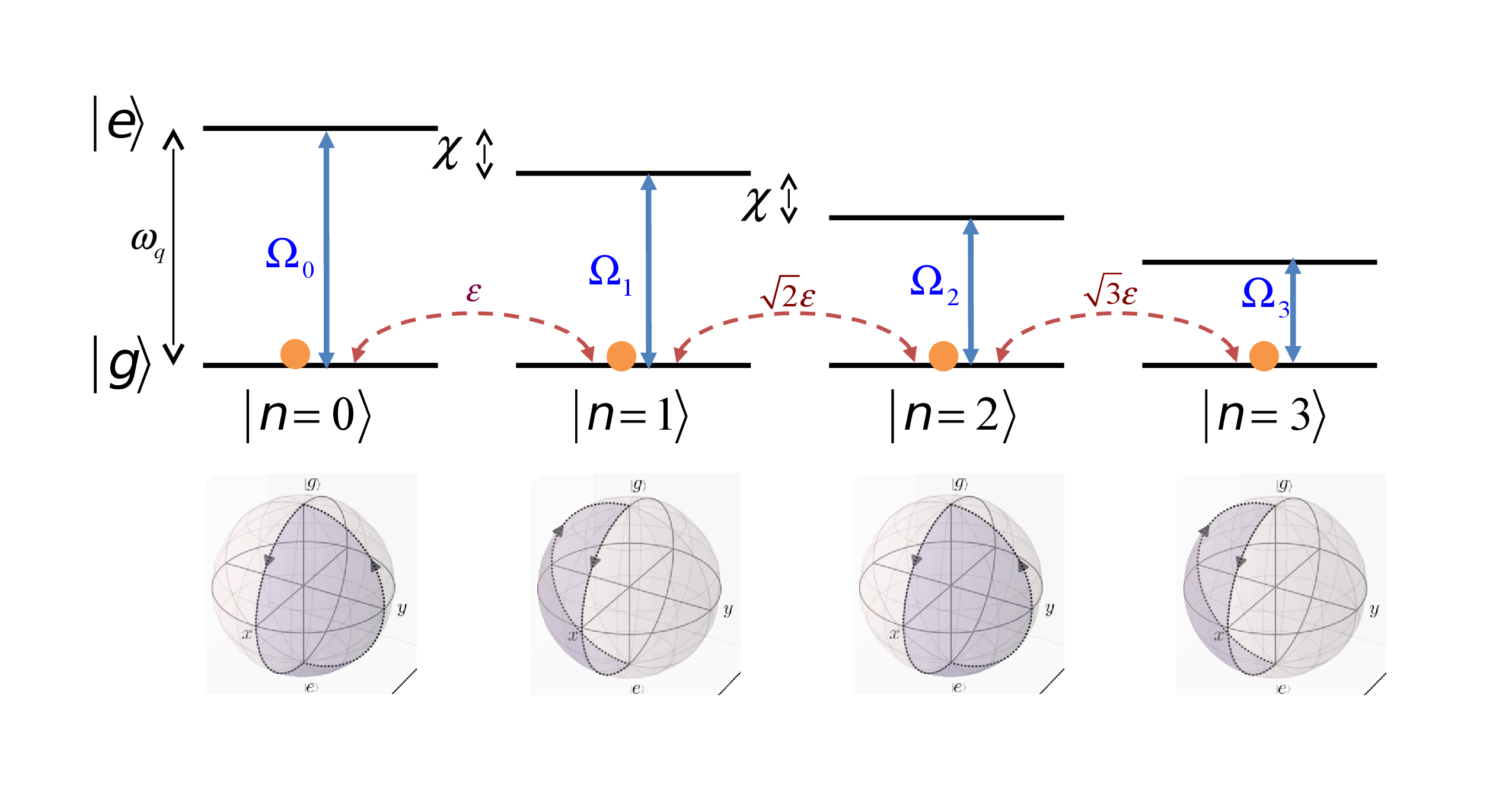
"SNAP" Gate

Selective on Number Arbitrary Phase

On one two-level subsystem:

• \(\hat{S}_{n}\left(\theta_{n}\right)=e^{i\theta_{n}\left|n\rangle\langle n\right|}\)

On all two-level subsystems at once:

• \(\hat{S}\left(\vec{\theta}\right)\,=\sum_{n=0}^{\infty}e^{i\theta_{n}}\mid n\rangle\langle n\mid\)

Proof of Universality

• Displacement: \(\hat{D}(\alpha)=\exp\left(\alpha\hat{a}^{\dagger}-\alpha^{*}\hat{a}\right)\)

• SNAP Gate: \(\hat{S}\left(\vec{\theta}\right)\,=\sum_{n=0}^{\infty}e^{i\theta_{n}}\mid n\rangle\langle n\mid\)

The group commutator of SNAP gates and Displacements can couple any neighboring pair of number states:

Explicit Algorithm - n to n+1

How to perform \(\left|n\right\rangle \rightarrow \cos(\theta)\left|n\right\rangle + \sin(\theta)\left|n+1\right\rangle\) ?

Explicit Algorithm - n to n+1

\(\hat{U}_{n}=\hat{D}(\alpha_{1})\hat{R}_{n}\hat{D}(\alpha_{2})\hat{R}_{n}\hat{D}(\alpha_{3})\)

\(\hat{R}_{n}=-\sum_{n'=0}^{n}\left|n'\rangle\langle n'\right|+\sum_{n'=n+1}^{\infty}\left|n'\rangle\langle n'\right|\)

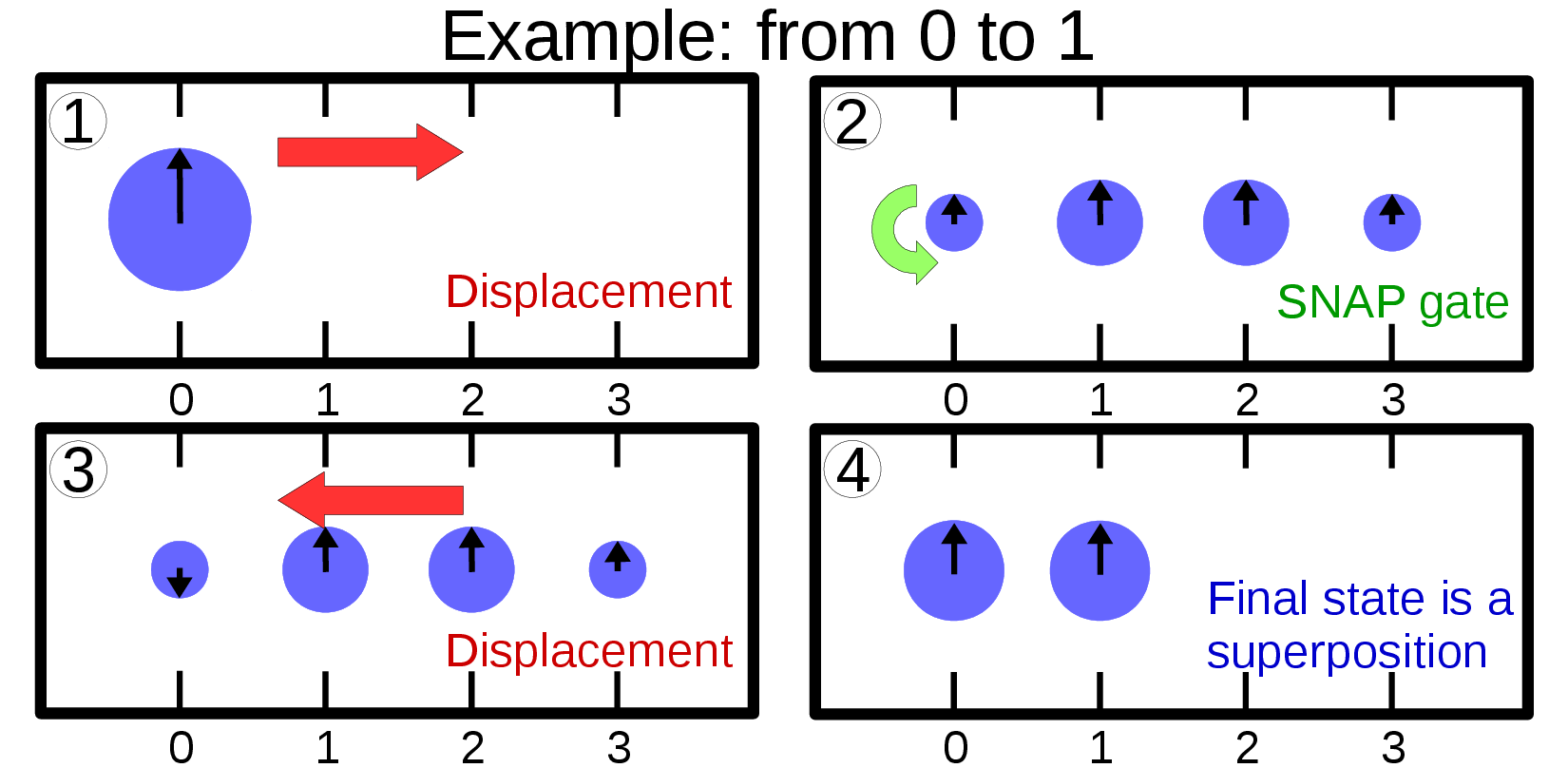
Universal Control

Use the 2D rotations to prepare each column of the matrix one by one.

N-by-N Unitary Matrix

We want to construct \(\hat{U}_{target}\)

\(\hat{U}_{target}^{-1}=\left[\begin{array}{c|c} \hat{W}_{n\times n} & 0\\ \hline 0 & Id \end{array}\right]\)

N-by-N Unitary Matrix - Removing a Column

Chain \(N-1\) 2-dimensional rotations:

\(\hat{V}_{n-1,n}\dots\hat{V}_{1,2}\hat{S}_{n}\hat{U}_{target}^{-1}=\left[\begin{array}{c|c} \begin{array}{c|c} \hat{W}_{n-1\times n-1} & 0\\ \hline 0 & 1 \end{array} & 0\\ \hline 0 & Id \end{array}\right]\)

N-by-N Unitary Matrix

We repeat the procedure for all columns optimizing the fidelity

\(F=\left|\frac{1}{N_{cutoff}}Tr\left(\hat{U}^{\dagger}\hat{U}_{target}\right)\right|\)

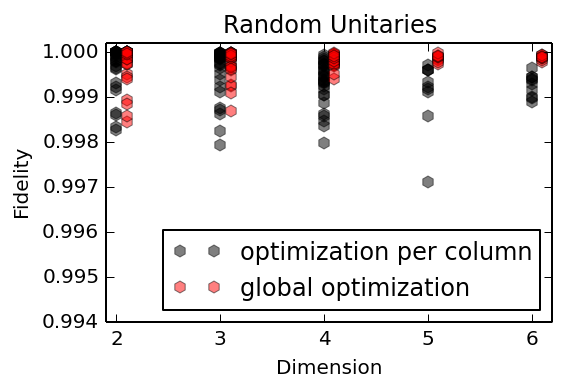
N-by-N Unitary Matrix

Fidelity for a random sample of unitary matrices:

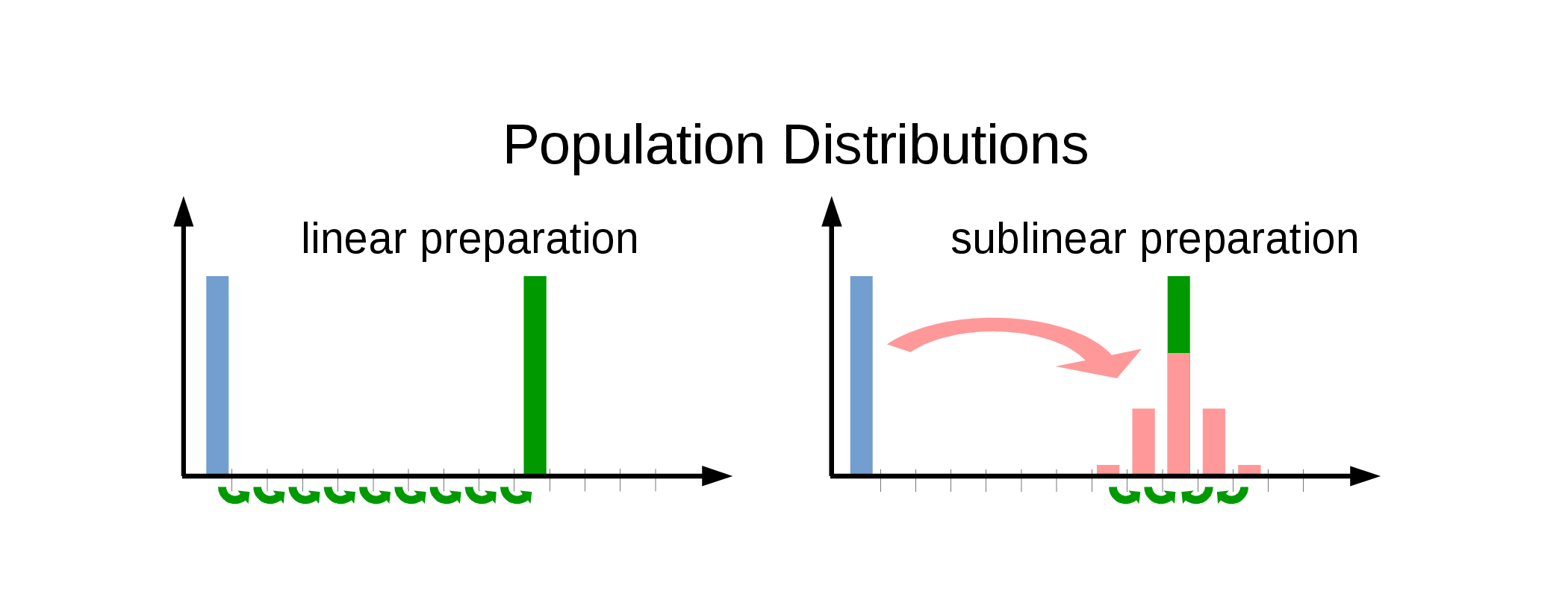
Super Efficient Fock State Preparation

• Displace to coherent state \(\mid\alpha\rangle=D(\alpha=\sqrt{n})\mid0\rangle\)
• Use \(\mathcal{O}(\sqrt{n})\) rotations to "fold" it into \(\mid n \rangle\)

Tally the Cost

• To perform an arbitrary N-by-N unitary matrix
  • \(\mathcal{O}(N^2)\) gates neccessary
• To prepare a state with an N-dimensional cutoff:
  • \(\mathcal{O}(N)\) gates neccessary
  • \(\mathcal{O}(\sqrt{N})\) gates neccessary for "sparse" states

Asymptotic Fidelity

Consider again 2D rotations and look at small \(\theta\):

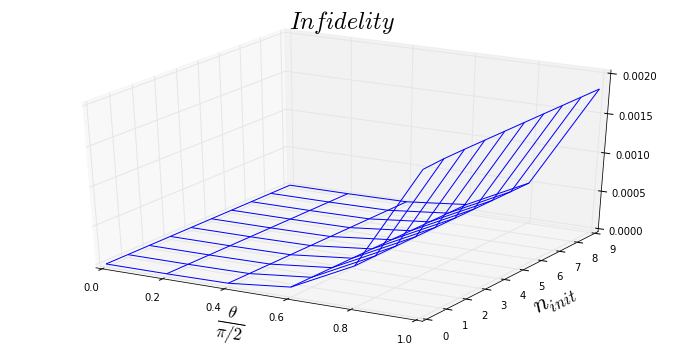
Asymptotic Fidelity

We can prove

\(\text{#gates} \propto \frac{N^3}{\sqrt{\text{infid}}}\)

\(\text{Time} \propto \frac{N^3}{\sqrt{\text{infid}}} \frac{1}{\chi}\)

Conclusion

arXiv preprint 1502.08015 (and experiment at 1503.01496)

• Efficient State Preparation
  • Including an Optimization for Fock States
• Efficient Universal Control
  • Satisfactory at "first-pass" level
  • Remains Efficient in the Asymptotic Regime
• People are Already Implementing it in Schoelkopf's group at Yale
  • Y39.00005 (by Reinier Heeres in 20 minutes)